ما هي اللوغاريتمات وما تطبيقاتها؟
هل تتذكر العمليات الحسابية مثل القسمة المطولة أو عملية الضرب التي تتكون من ضرب رقم أو أكثر في رقمين أو ربما أكثر. والتي قد تكون عقدة في حياة البعض من الطلاب في المرحلة الإبتدائية تحديدًا لوقتنا هذا. حيث أجرى العلماء عامة وعلماء الرياضيات خاصة، حساباتهم بتلك الطرق لمئات السنين والتي كانت تستغرق منهم وقتًا طويلًا. إضافةً إلى الاحتمالية في الخطأ. وقد استُبعدت هذه العمليات من علوم كثيرة لهذا السبب على سبيل المثال علم الفلك والملاحة وغيرها. لكن اكتشاف اللوغاريتمات حل مشكلة عدم الدقة وأحدث ثورة. وفي هذه المقالة سنناقش المعادلات اللوغاريتمية والتي هي جزء من سلسلتنا عن أشهر المعادلات الرياضية في التاريخ.
محتويات المقال :
كيف ظهرت اللوغاريتمات؟
ظهرت اللوغاريتمات من خلال مقارنة المتواليات الحسابية والهندسية. حيث يشكل كل حد نسبة ثابتة مع الذي يتبعه. فمثلًا:
.. 1/1000, 1/100, 1/10, 1, 10, 100, 1000 ..
في المتتالية الهندسية السابقة، النسبة المشتركة هي 10.
والآن لاحظ هذه المتتالية:
… 3, 2 ,1 , 0, 3- ,2- ,1- …
هنا الفرق المشترك هو 1، وهذه هي المتتالية الحسابية -التي تعتمد على الفرق والجمع-، على عكس المتتالية الهندسية -التي تعتمد على القسمة والضرب-.
كذلك يمكن كتابة التسلسل الهندسي للمتتالية الأولى على النحو التالي:
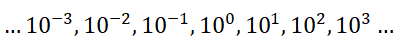
فضرب رقمين في المتتالية الهندسية مثل 10/1 و100، سيساوي جمع الأسس للنسبة المشتركة 1- و2؛ للحصول على:
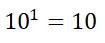
وبالتالي يتساوى الضرب مع الجمع، لكن على الرغم من ذلك فإن المقارنة الأصلية بين المتتاليتين لم تستند على أي استخدام صريح للتدوين الأسي. لذا نشر عالم الرياضيات السويسري «جوست بورجي-Joost Burgi» عام 1620 أول جدول يستند على مفهوم ربط المتتاليات الهندسية والحسابية.

من هو مكتشف اللوغارتيمات؟
نشر عالم الرياضيات الاسكتلندي «جون نابير-John Nabier-» عام 1614 جدوله الخاص باللوغاريتمات، حينها أحدث هذا الاكتشاف ثورة في العمليات الحسابية. كذلك وبشكل مستقل، يُقال أن عالم الفلك الشهير يوهان كيبلر اكتشف اللوغارتيمات أيضًا. لكن نابير هو من نشر أولًا. وكان هدف نابير المساعدة في مضاعفة الكميات التي كانت تسمى الجيب. كان الجيب هو قيمة ضلع مثلث قائم الزاوية به وتر كبير. وبالتعاون مع عالم الرياضيات الإنجليزي هنري بريجز، قام نابير بتعديل اللوغاريتمات الخاصة به إلى شكلها الحديث.

توفي نابير في عام 1617 واستمر بريجز بمفرده، وجاء علماء من بعده مثل الهولندي «أدريان فلاك-Adriaan Vlacq» ومصطلح اللوغاريتمات مصاغ من الكلمات اليونانية logos (نسبة) وarithmos (عدد).
ما هي اللوغارتيمات؟
تُعرّف اللوغاريتمات على أنها طريقة أخرى للتفكير في الأسس، حيث تربط التقدم الهندسي بالتقدم الحسابي. إذ تصف اللوغاريتمات كيف يفكر البشر غريزيًا في الأرقام. وبشكل أخر إن اللوغاريتم هو عبارة عن عملية حسابية تحدد عدد المرات التي تم فيها ضرب رقم معين -يُسمى الأساس- في نفسه وصولًا إلى رقم آخر (كمعرفة عدد المرات التي تحتاجها لطيّ ورقة للحصول على 64 طبقة).
مثال: إذا كان الرقم 2 (الأساس) مضروب في 4 (الأس) فعلينا ضرب 2*2*2*2 لتساوي 16، فإن التعبير عن ذلك من خلال المعادلة الأسية يكون:
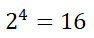
ولنفترض أن شخص سألك بصيغة أخرى، ما الرقم الذي إذا رفعناه للرقم 2 (أي أس 2) يكون الناتج 16؟ سيكون جوابك 4. ويتم التعبير عن ذلك بالمعادلة اللوغارتيمية:
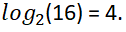
وتُقرأ لوغارتم 16 للأساس 2 يساوي 4.
ما هي أنواع اللوغاريتمات؟
– اللوغاريتم المشترك
يُعرف باسم اللوغاريتم العشري أو العام أو briggsian (نسبة إلى عالم الرياضيات الإنجليزي «هنري بريغز-Henry Briggs»، حيث يحدد اللوغاريتم المشترك عدد المرات التي مطلوب فيها ضرب الرقم 10 للحصول على الناتج بمعنى آخر لوغاريتم أي عدد بالنسبة للأساس (الثابت) عشرة). ويكتب على هذا النحو:
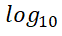
وأحيانًا يكتب بدون الأساس عشرة وستجدها في الآلة الحاسبة حيث يشير عدم وجود أساس أن الأساس عشرة.
اللوغاريتم الطبيعي
اللوغاريتم الطبيعي (ln) -الذي يحدد كم علينا ضرب العدد e للحصول على الناتج المطلوب- حيث e ثابت أويلر الذي يساوي 2.71828.
تُعرّف دالة اللوغاريتم الطبيعي بواسطة:
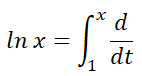
x > 0، فهو مشتق من:
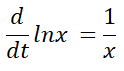
قواعد اللوغاريتمات
قاعدة الضرب
توضح تلك القاعدة أن ضرب اثنين من اللوغاريتمات ببعضهما يساوي مجموعهما.
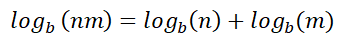
على سبيل المثال:
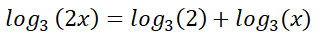
قاعدة القسمة
توضح تلك القاعدة أن قسمة اثنين من اللوغاريتمات تساوي طرحهم.
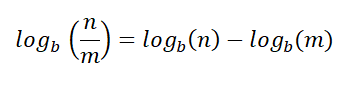
على سبيل المثال:
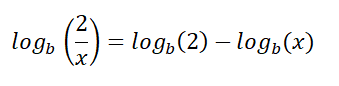
القاعدة الأسية
توضح تلك القاعدة أن لوغاريتم أي رقم مرفوع لأس يساوي الأس مضروبًا في لوغاريتمه.
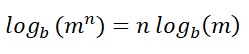
على سبيل المثال:
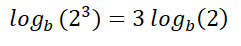
قاعدة تغيير أساس اللوغاريتمات
توضح تلك القاعدة أنه يمكننا تغيير أساس اللوغاريتم.
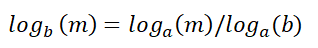
على سبيل المثال:
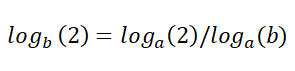
قاعدة تبديل أساس اللوغاريتمات
توضح تلك القاعدة أنه يمكننا تبديل الأساس.
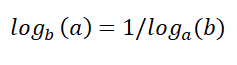
على سبيل المثال:
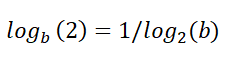
بعض قواعد الإضافية:
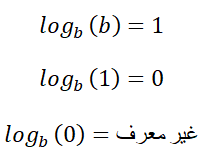
تطبيقات اللوغاريتمات
تطبيقات اللوغاريتمات عديدة وقد ذكرنا أن الهدف منها تبسيط الاحصاءات التي تحتوي على أرقام كبيرة جدًا أو صغيرة جدًا فحتى بعد اختراع الآلات الحاسبة والحواسيب العملاقة ما زالت اللوغاريتمات مستخدمة لوقتنا، فتدخل اللوغاريتمات في معظم العلوم مثل علوم الحاسوب والكيمياء والفيزياء وبالطبع الرياضيات وفي حياتنا اليومية وإليك بعض الأمثلة.
– مثال من حياتنا، إذا أردت تحديد هل قيادة الدراجات بدون خوذة مخاطرة أقل أم القفز بالحبال في وادي ما، فستجد بيانات متوفرة مثل أن 20 ألف شخص يتوفى بسبب عدم ارتداء خوذة، كذلك لديك معلومة أخرى وأن مائة ألف شخص يتوفى بسبب القفز بالحبال. فهل هكذا القفز بالحبال أكثر أمانًا؟ إن الأرقام الكبيرة صعب معالجتها في أدمغتنا. لذا اللوغاريتمات تحل ذلك، فهيا لنستخدمها. حيث يمكننا وضع مقياس مثلًا من 1 لـ 10. فيكون 1 هو الأكثر خطورة و10 الأكثر أمانًا. فيمكننا التعبير عن ذلك بأن لوغاريتم 20 ألف للأساس عشرة وهذا سيساوي 4.3 ولوغاريتم 100 ألف للأساس عشرو سيساوي خمسة. وسنستنج بطريقة منطقية وخالية من الاحتمال ودقيق أن القفز بالأحبال أكثر أمانًا بقليل من ركوب الدرجات بغير خوذة. هذا دور الخوارزميات وهذا مثال بسيط حيث تظهر أهميتها ودقتها أكثر في احصائيات صعب استيعاب ارقامها وفي علوم تحتاج لدقة.
– مثال آخر من الكيمياء، إذا أردت معرفة حموضة أو قلوية مادة ما فاللوغاريتمات ستساعدك. فعلى سبيل المثال يحتوي الماء على 1*10 أس 7- مول من أيونات الهيدروجين لكل لتر، فهل هو حامضي؟ لذا هناك مقياس وهو الأس الهيدروجيني الذي يعالج الأعداد الصغيرة جدًا. ويتراوح بين 0 و14. فالماء محلولًا متعادلًا برقم هيدروجيني 7. لذلك المقايس التي تضعها اللوغاريتمات هي حل لرؤى واضحة.
المصادر
Explaining Logarithms: A Progression of Ideas Illuminating an Important Mathematical Concepts, Dan ,UmbargerBrown Books Publishing Group (January 1, 2006), P (1:25)
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.



التعليقات :