خوارزمية الخفاش، الخوارزمية الثورية المستوحاة من البحث بالصدى

الخفافيش حيوانات مذهلة. فإضافة لكونها الثدييات الوحيدة المجنحة، لديها قدرة متقدمة أيضًا على تحديد واستكشاف محيطها بالصدى. ويقدر أن هنالك حوالي 1000 نوع مختلف من الخفافيش، وتمثل ما يصل إلى 20٪ من جميع أنواع الثدييات. ووزن الخفاش يتراوح من حوالي 1.5 غرام – إلى غرامين ما يمثل الخفافيش الصغيرة – إلى ما يتجاوز الكيلوغرام، أي الخفافيش العملاقة ذات الأجنحة التي يناهز طولها، عند التمدد، المترين.

تستخدم معظم الخفافيش قدرتها على الاستشاعر و التوجه بالصدى بنسب متفاوتة في حياتها اليومية. لكن بين كل أنواعها، الخفافيش الصغيرة Microchiroptera أو Microbats هي الأكثر اعتمادًا واستخدامًا لهذه القدرة. في حين أن الخفافيش الكبيرة نسبيًا والخفافيش العملاقة Megachiroptera لا تستعملها كثيرًا، أو قد تستغني عنها تمامًا.

معظم الخفافيش الصغيرة آكلة حشرات. وتستعمل في نشاطاتها اليومية نوعًا من أنواع السونار، أو ما يسمى بالإنجليزية Echolocation وتعني تحديد الموقع بالصدى. فتستخدم قدرتها هذه في البحث عن فريستها، وتحديد موقع جحورها. وكذلك استكشاف محيطها لتجنب المعوقات والعقبات.

هذه الخفافيش تطلق صوتًا مرتفعًا، فتصطدم هذه النبضات الصوتية وترتد عن الأجسام المحيطة ممكنةً الخفافيش التي أصدرتها من التقاطها مرة وأخرى. الشيء الذي يخولها إمكانية تصور محيطها بطريقة ثلاثية الأبعاد. وتختلف هذه النبضات في حدتها ومستواها من نوع لأخر، أو مجموعة لأخرى. بحيث أنها قد تعتمد أيضًا على استراتجية المجموعة في الصيد.

تظهر الدراسات أن الخفافيش الصغيرة تستخدم التأخر الزمني بين إصدار الصوت وإلتقاط الصدى. كما تستخدم الفرق الزمني بين الالتقاط من أذن إلي أخرى، واختلافات مستوى الصدى لبناء بنية ثلاثية الأبعاد لمحيطها. ما يمكنهم من التعرف على المسافة، واتجاه الهدف، ونوع الفريسة، وحتى سرعة حركة الفريسة – والتي غالبا ما تكون حشرات صغيرة. وما يدعو للعجب هو أن الدراسات والملاحظات تشير إلى كون الخفافيش الصغيرة قادرة على التمييز بين الفرائس التي تستهدفها انطلاقًا من تأثير دوبلر Doppler المولد بفعل حركة أجنحة هذه الحشرات. فيعني هذا عمليًا أن الخفافيش تبصر باستخدام الصوت، وليست في حاجة لابصار شيء. هذا ما يفسر ميلها نحو النشاط الليلي رغم قدرتها على الإبصار نهارًا. وذلك رغم عدم قدرتها على الرؤية ليلًا مثل القطط والحيوانات الليلية الأخرى.

خصائص البحث بالصدى

رغم استمرار نبضات الصدى لأجزاء قليلة من الألف من الثانية، من 8 إلي 10 مللي ثانية، فإن لها ترددًا ثابتًا يتراوح بين 25 كيلو هرتز و150 كيلو هرتز. عمومًا نجد متوسط هذا التردد عند أغلب أنواع الخفافيش بين 25 و 100 كيلو هرتز. في حين أن أنواعًا قليلة فقط تصل ل 150 كيلو هرتز.
تختلف مدة استمرار النبضات وعددها حسب الظروف والنوع. فنجد أن الخفافيش الصغيرة تستطيع إصدار ما يتراوح بين 10 و 20 نبضة فوق صوتية خلال كل ثانية. هذه النبضات قادرة على الاستمرار بين 5 و 20 جزء من الألف من الثانية. لكن عند عملها على اصطياد فريستها واقترابها منها، قد يتسارع عدد هذه النبضات لما قد يصل إلي 200 نبضة فوق صوتية في الثانية الواحدة. وإن دل كبر هذا العدد على شيء فإنه يدل على مدى قوة قدرة أدمغة هذه الخفافيش على معالجة هذا الكم الكبير من المعلومات بهامش زمني صغير، وأن لها أذانًا جيدة للغاية. فتجد الدراسات أن وقت دمج أذن الخفافيش integration time يتراوح بين 300 و400 مللي ثانية. لكن أذان البشر أفضل بوقت دمج لا يتجاوز 100 جزء من الألف من الثانية.

نظرًا لكون سرعة الصوت في الهواء عند درجة حرارة الغرفة، أي 20 درجة سيلسيوس، تقارب 340 متر في الثانية. فإن الطول الموجي λ لكل نبضة يتراوح بين 2 و 14 مللي متر. باعتبار ترددها بين 25 و 150 كيلو هرتز. من الواضح أن هكذا أطوال موجية تجاور أطوال وأحجام فرائس هذه الخفافيش. والمثير للدهشة حقًا هو أن النبضات المنبعثة يمكن أن تعلو ويصل مستواها ل 110 ديسيبل. وكذلك من حسن حظ هذه الخفافيش أن تردد أصواتها يوجد في منطقة الموجات فوق الصوتية، إذ كانت لتباد من قبل البشر الأوائل أو حتى قبل ذلك من المفترسات الأخرى، فصوت بتلك الحدة ليس مزعجًا فقط بل وقد يسبب إجهادًا نفسيًا.

نجد كذلك أن مستوى الصوت يختلف من مرتفع عند البحث عن طريدتها إلي منخفض عند إيجادها لهذه الفريسة وتعقبها إياها. كما أن مدى هذه الموجات لا يتجاوز أمتارًا معدودة، الشيء الذي يعتمد على التردد. إضافة لكون الخفافيش قادرة باستعمال الصدى على مراوغة معوقات بصغر شعرة رأس إنسان.

ومن المعلوم أن لبعض الخفافيش بصر جيد، كما أن لمعظمها حاسة شم حساسة للغاية. وتستخدم الخفافيش جميع حواسها معًا لتحقيق أقصى قدر من الكفاءة للكشف عن الفريسة والتنقل السلس. لكن ما يهمنا حقًا هنا هو فقط قدرتها لتحديد الموقع بالصدى والسلوكيات المرتبط به. انطلاقًا من هذا، يمكن صياغة ألية بحثها بالصدى بطريقة تمكننا من ربطها بالدالة الهدف للمشكل التحسيني. ما يمكننا بالطبع من إنتاج عدد من الخوارزميات التحسينية بواسطتها.

استنباط آلية عمل خوارزمية الخفاش

إن استنبطنا بعضًا من خصائص آلية بحث الخفافيش بالصدى، يمكننا تطوير عدد من الطرق الخوارزمية الصالحة للتطبيق في مواجهة المشاكل التحسينية. ومن أجل هذا، يمكن أن نخلص لثلاث أفكار رئيسية، وهي المفاهيم التي ستعتمدها خوارزمية الخفاش في تنفيذها:

1. جميع الخفافيش قادرة على إدراك المسافة التي تفصلها بين الأجسام التي تحيط بها. كما أنها أيضًا قادرة على التمييز بين هذه الأجسام، إن كانت طرائد أو فقط معوقات.
2. تحلق الخفافيش بسرعة معينة قد تختلف من نقطة لأخرى. إضافة لإمكانية تعديل تردد موجات نبضاتها، وبالتالي الطول الموجي، و كذلك التحكم في عدد النبضات في الثانية.
3. ورغم إمكانية تغيير مستوى الصوت بطرق مختلفة إلا أننا نفترض تغيره بين قيمتين A 0 موجبة وA min سالبة.

آلية عمل خوارزمية بحث الخفاش

حركة الخفافيش

عند محاكاة هذه الآلية يتوجب علينا تعريف الخفافيش الافتراضية. وذلك بوضع قواعد تحدد كيفية تغير وتحديث مواضعها وسرعاتها في فضاء مستمر متعدد الأبعاد. الشيء الذي يمكننا تحقيقه استنادًا لعدد من الصيغ والمعادلات، وهي كالتالي:

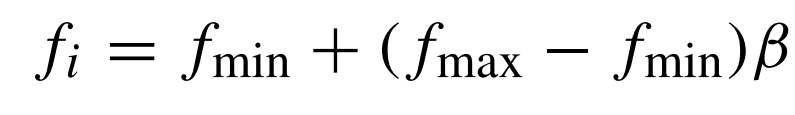
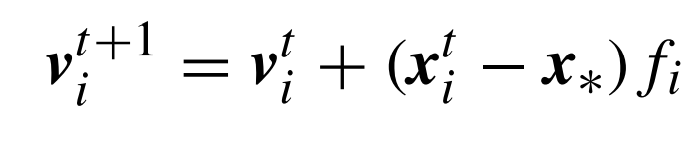
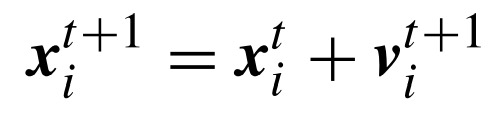
لكون الفضاء المدروس متعدد الأبعاد فإننا نتعامل مع متجهات، نجد بيتا عبارة عن متجهة عشوائية من التوزيع المنتظم، ذات مقادير محصورة بين 0 و 1. وتمثل *X الحل الحالي الأمثل والذي نحصل عليه بعد مقارنة جميع الحلول التي وجدتها الخفافيش الافتراضية. ولكون التردد والطول الموجي، والذي هو سرعة الصوت، ثوابت، يمكننا استخدام أي منهما في المعادلة الثانية من أجل ضبط تغير السرعة. وفي التنفيذ، يمكن وضع f min = 0 كمقدار أدنى للتردد و f max = O(1) انطلاقًا من حجم فضاء البحث. وعند وضع الخفافيش الافتراضية، يتم منحهم قيم تردد موزعة بين القيمتين الدنيا والقصوى.

وفيما يخص البحث المحلي، فعند انتقاء الأفضل بين الحلول الحالية التي يقدمها كل خفاش، يتم توليد حل عشوائي جديد لكل واحد انطلاقًا من صيغة سير عشوائي random walk وتكون كالتالي:

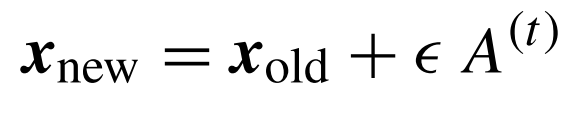
من وجهة نظر تنفيذية، يستحسن إضافة معلمة σ لتحجيم مدى الخطوة. وبالتالي تتغير معادلة السير العشوائي للصيغة التالية:

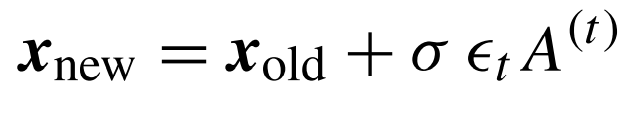
مستوى الصوت وإصدار النبضات

عند كل دورة تكرار، يجب تحديث قيم مستوى الصوت A0، و معدل إصدار النبضات ri وفقًا لبعضها البعض. وذلك لكون خفض الخفافيش لمستوى الصوت المنبعث عند اقترابها من فريستها. كما تزيد من عدد النبضات التي تصدرها خلال الثانية الواحدة. ولا يوجد شرط أو مانع من تحديد قيم مختلفة لمستوى الصوت بدئيًا في كل تنفيذ، فيمكننا اختيار A0 = 1 و A min = 0. ما يعني افتراضًا أن الخفاش بدئيًا يكون بقرب فريسته ويتوقف مؤقتًا عن إصدار أي صوت. ويمكن تلخيص كل هذا اعتمادًا على الصيغ التالية:

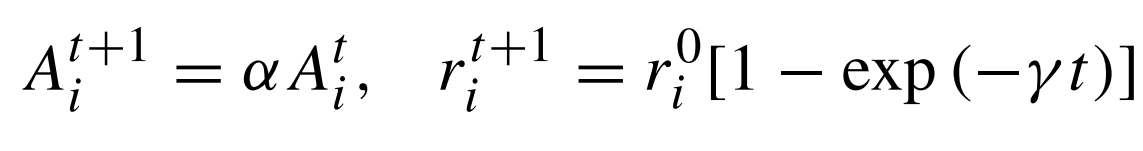
بحيث نجد أن ألفا α و غاما γ ثوابت. وهذه الثوابت تشبه نظيرتها في خوارزمية التخمير المحاكى بحيث يمكن تشبيه ألفا بمعدل التبريد في جدولة التلدين. فلكل 1>ألفا>0، و 0<غاما، نجد:

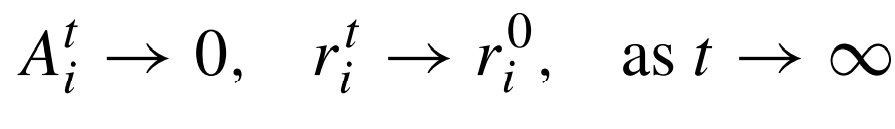
وتتطلب عملية اختيار معلمات الضبط بعضًا من التجربة والخطأ. فبدئيًا يجب أن يصدر كل خفاش مستوى صوت مختلف، مما يمكن الوصول إليه باعتماد العشوائية. فيمكننا، على سبيل المثال، أخد 1 كقيمة بدئية لمستوى الصوت و مقدار أخر بين 0 و 1 كقيمة لمعدل النبضات. وسيتم تحديث هذه القيم فقط عند تحسن قيمة الحل الأفضل الحالي، مما يعني اقتراب أحد الخفافيش من فريسته، أي في حالتنا هذه الحل الأمثل.

تحليل التقارب

قام جورج هوانغ G.Q. Huang وزملاؤه ببحث تفصيلي ومعمق لتحليل آلية تقارب خوارزمية الخفاش وذلك باستخدام نظرية معالجة ماركوف المتناهية finitie Markov process theory. ما مكنهم من أن يخلصوا لكون خوارزمية الخفاش تحقق جميع شروط ضمان التقارب للحل الأمثل في تحسين الدوال الهدف غير المقيدة Unconstrained objective functions. وبالنسبة للدوال المقيدة وغير الخطية، تتقارب هذه الخوارزمية للحل الأمثل باستعمال ضبط معين، initialization of orthogonal Latin squares.

واقترح الفريق أيضًا متحورًا مغايرًا بسرعة تقارب أعلى، وأطلقوا عليه اسم خوارزمية الخفاش المعدلة Modified Bat Algorithm، أو اختصارا MBA. كما بينوا أيضا قدرة هذا المتحور على مواجهة المشاكل التحسينية الضخمة بكفاء أعلى.

متحورات خوارزمية الخفاش

تعمل خوارزمية الخفاش الأساسية بشكل جيد في مواجهة الدوال الهدف المستمرة. ولكن للتعامل مع المشاكل ذات الدوال غير المستمرة ومعالجة المشاكل التوافقية، نجد أن هنالك حاجة إلى بعض التعديلات وابتكار متحورات جديدة. لذلك طور ناكامورا وزملاؤه الباحثين ما يسمى بخوارزمية الخفاش الزوجية Binary Bat Algorithm، أو اختصارًا BBA. من أجل حل هذة المشكلة لمواجهة الدوال الهدف المتقطعة.

ومن أجل غايات وأهداف مماثلة نجد العديد من المتحورات مختلفة الاستعمالات مثل:

• خوارزمية خفاش المنطق الضبابي Fuzzy Logic Bat Algorithm.
• خوارزميات الخفاش متعددة الأهداف Multi-objective Bad Algorithm، من طرف نفس مطور خوارزمية الخفاش الأصل شين شي يانغ.
• خوارزمية الخفاش الفوضوية Chaotic Bat Algorithm.

بالإضافة إلى العديد من المتحورات والامتدادات الأخرى.

تطبيقات خوارزمية الخفاش

يرجع تعدد متحورات خوارزمية الخفاش في الأساس لقوتها ومدى فعاليتها. فنجد أنه منذ تطويرها في سنة 2010 من طرف عالم الرياضيات والحاسوب شين شي يانغ Xin She Yang، تم استخدامها في كل مجالات التحسين الحوسبي. كما تم دراسة فاعليتها في مواجهة أغلب المشاكل التحسينية المعروفة. ومن بين هذه التطبيقات نجد:

• معالجة المشاكل التحسينية المستمرة مثل التصميم الصناعي والهندسة المعمارية.
• تحسين المشاكل التوافقية والجدولة، ما يمكن من حل مختلف مشاكل NP الصعبة.
• المشاكل المعاكسة وتقدير المعلمات، مثل مشاكل تصميم الإلكترونيات الدقيقة وتدبير نقل الحرارة.
• معالجة الصور والذكاء الاصطناعي.

مصادر

1. Nature Inspired Optimization Algorithms by Xin She Yang