- ما هي الخوارزميات المستوحاة من الطبيعة واستخداماتها ؟
- الساكنة البدئية في الخوارزمية التحسينية وأهميتها؟
- كيف يتم اختيار الخوارزميات التحسينية ؟
- ما هي الخوارزميات الجينية؟
- تعرف على خوارزمية النزول التدرجي الأشهر في الخوارزميات التحسينية
- ما هي خوارزميات التخمير المحاكى وكيف تعمل؟
- لم استوحت خوارزمية البحث التناغمي من الموسيقى وكيف تعمل؟
- خوارزمية التطور التفاضلي، الخوارزمية المستوحاة من نظرية التطور!
- خوارزمية الخفاش، الخوارزمية الثورية المستوحاة من البحث بالصدى
- ما هي خوارزمية مستعمرة النمل Ant Colony Algorithm وكيف تعمل؟
- خوارزميات النحل، الخوارزميات الثورية في مجال الحوسبة التحسينية
- دليلك لفهم خوارزمية أدم ADAM التحسينية الأكثر استخدامًا في التعلم العميق
خوارزميات التخمير(التلدين) المحاكى simulated annealing هي أحد أقدم الخوارزميات المستوحاة من الطبيعة و كذلك من أكثرها استخدامًا. وتعتمد في عملها على البحث العشوائي لبناء مسارات تأخدنا للحل الأمثل. وتحاكي خوارزميات التخمير عملية التلدين في معالجة المواد المعدنية. ففي الصناعات المعدنية، تتميز عملية التخمير بعدد من الخصائص مثل درجة الحرارة و سرعة التبريد. ويخلق هذين المفهومين حرفيًا نتيجة العملية الصناعية، بحيث يحددان الجودة والتركيبة الكريستالية للمعدن الناتج. أي بأقل استهلاك طاقي، وأكبر حجم بلورات، وأقل كم من الشوائب.
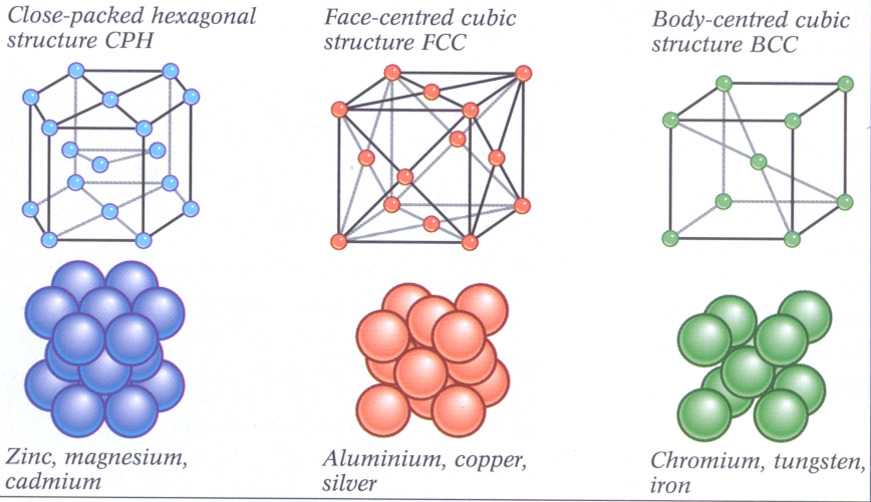
تسمى هذه العملية (عملية التلاعب الدقيق في درجة الحرارة و معدل التبريد) بجدولة التلدين.
محتويات المقال :
آلية عمل خوارزميات التخمير المحاكى
منذ أن تم تطوير خوارزميات التلدين المحاكى simulated annealing أول مرة من طرف كيركباتريك S. Kirkpatrick وزملائه، تم تطبيقها في مختلف مجالات الحوسبة التحسينية optimization. فأتت الاستعارة أو المجاز في تسمية هذه الخوارزميات من خصائص التلدين في معالجة المعادن وذلك رغم أن هذه الخوارزميات، في جوهرها، تشبه أكثر خوارزميات متروبوليس الكلاسيكية التي تم تطويرها من طرف نيكولاس ميتروبوليس N. Metropolis وزملائه.

أفضلية خوارزميات التلدين المحاكى
على خلاف الخوارزميات التي تتبنى، في معالجة مدخلاتها، طريقة تدرجية gradient-based approach. و الخوارزميات البحثية القطعية deterministic search methods، التي تخسر إثر وقوعها في حل محلي local optima وتفقد قدرتها على التقارب باتجاه الحل الأمثل global optima. تمتاز خوارزميات التخمير المحاكى بقدرتها على تجنب الوقوع في هذه المشكلة. وقد ثبث ذلك تجريبيًا، فخوارزميات التخمير المحاكى دائمًا ما تتقارب نحو الحل الأمثل global optima إن تم توفير عشوائية كافية وسرعة تبريد بطيئة معًا. يرجع هذا جزئيًا لكون هذه الخوارزميات تعتمد سلسلة ماركوف Markov chain التي توفر إمكانية التقارب عند تحقق شروط معينة.
مجازًا، تكافئ عملية التقارب هذه إسقاط عدد من الكرات المطاطية المرتدة فوق مساحة إسمنتية ذات تضاريس متنوعة، بينما تقفز وترتد هذه الكرات فتخسر كم من طاقتها الحركية وبالتالي تتدحرج بعد عدد من الوثبات وتستقر في النقطة الأكثر إنخفاضًا في محيطها أي الحل المحلي الأمثل local optima. لكن إن تم تمكين هذه الكرات من الوثب لمدة أطول وخسارة طاقتها الحركية ببطء كاف، سنجد أن عدد منها لن يسقط فقط للحلول المحلية بل تسقط نحو أخفض نقطة على الإطلاق، أي أنها تتقارب نحو الحل الأمثل global optima. في حالتنا هذه نسمي هذا الحل بالحل الأدنى global minimum.
سلسلة ماركوف
الفكرة الأساس في خوارزميات التخمير المحاكى هي استخدام البحث العشوائي على شاكلة سلسلة ماركوف. وهذه السلسلة، سلسلة ماركوف، هي عبارة عن نموذج عشوائي stochastic model مبني على العمليات العشوائية. وتصف تلك العمليات العشوائية سلسلة من الأحداث الممكنة. بحيث كل حدث يعتمد احتمال حدوثه فقط على مخرجات سابقه، أي الحدث الذي قبله. في هكذا إطار، لا يحتاج التكهن بمستقبل الأحداث إلى الماضي بل فقط للحاضر. أي مخرجات الحدث الذي شهدناه، والمستقبل هو الحدث الذي يليه.
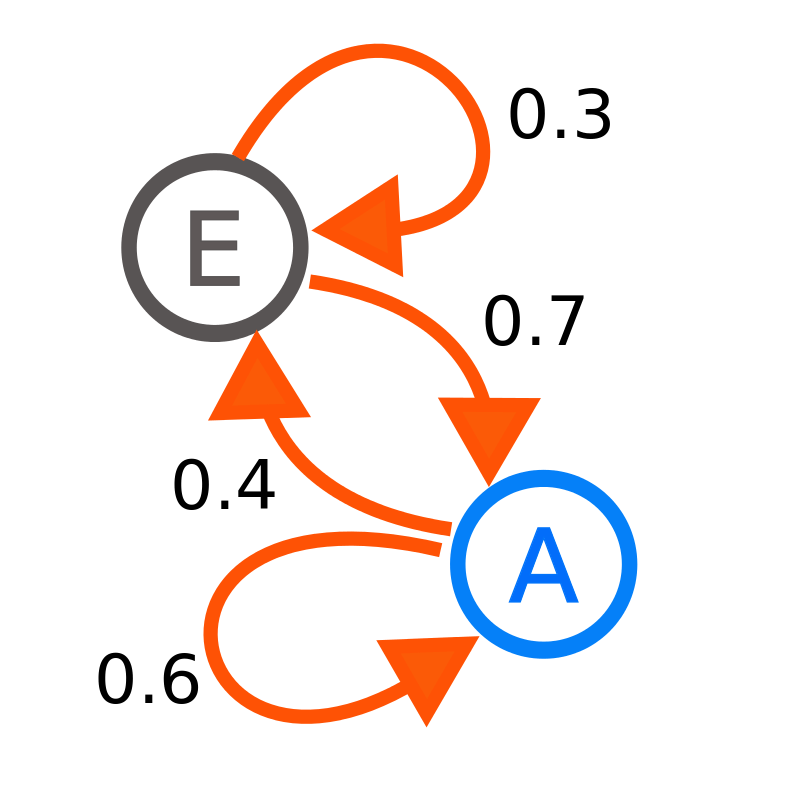
لكون خوارزميات التخمير المحاكى تستعمل في مقاربتها للوصول للعشوائية على سلسلة ماركوف، لا تبقي فقط على الحلول الأحسن في كل جولة تكرار بل أيضًا تحتفظ بعدد من الحلول التي لا تحسن الملائمة، أي حلول أسوء. و هذا أفضل نظرًا لتحقيقه عشوائية وتنوع فائقين.
هذا النهج ممنهج باستخدام دالة إحتمالية p، وهذه الدالة هي بالطبع التي تحدد احتمالية الانتقال من حدث لأخر أي في حالتنا هنا احتمالية قبول الحلول الأسوء إن صح التعبير. فإن لم يتم تقييد وتقنين طريقة الاختيار والإبقاء على الحلول الرديئة، فسنخلق فوضى غير مضمونة النتائج. أي سنضيع قدراتنا الحوسبية بلا فائدة. وبما أن هذه الخوارزميات في أساسها مبنية على نظرية فيزيائية طبيعية، وكل الظواهر الفيزيائية أو أغلبها منمذجة. نستطيع أن نستعمل كدالة احتمالية p المعادلة، المستلهمة من نظيرتها الفيزيائية في الديناميكا الحرارية، التالية:
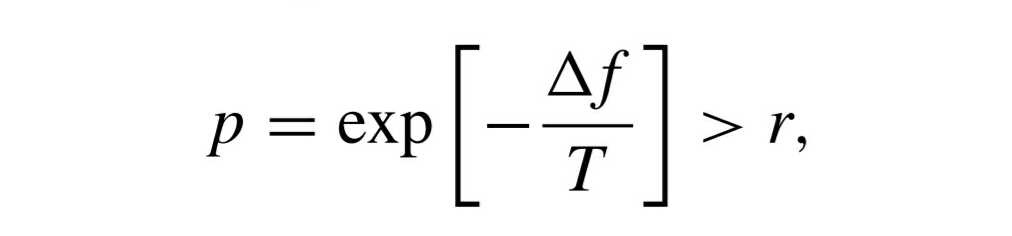
خطوات التنفيذ
الخطوة الأولى
نبدأ أولًا بوضع ساكنة بدئية S. و كذلك درجة حرارة بدئية T. يمكن اختيار هذه الحرارة ابتداءً من عدد كبير وتتناقص مع الوقت، لتصل إلى الصفر. أو نختارها من واحد وتتناقص إلي أجزاء من الصفر، على سبيل المثال من 1 إلي 0.00001.
الخطوة الثانية
وضع قاعدة تناقص درجة الحرارة. هذه الخطوة مهمة لأنها تحدد سرعة التبريد، والتي ناقشنا أهميتها سابقًا. قاعدة أو ‘دالة’ تناقص الحرارة يتم التوصل إليها حسب الحاجة. عمومًا هناك ثلاث طرق للوصول لهكذا دالة و هي بسيطة كالتالي:

1. التناقص الخطي
أي عند كل تكرارة تتناقص الحرارة بقيمة ‘ألفا’ محددة.
2. التناقص الهندسي
أي عند كل دورة، يتم ضرب قيمة الحرارة في معامل ألفا أصغر من واحد وأكبر من الصفر. يعني هذا أننا نقوم بإعدام قيمة الحرارة بنسبة معينة كل مرة. بحيث ‘ألفا’ تمثل النسبة التي سنبقي عليها عند كل تكرار. مثال: إن كانت ألفا تساوي 1/3 يعني أننا نبقي فقط على ثلث درجة الحرارة السابقة.
3. قاعدة التناقص البطيء
كونها تحمل هذا الإسم لا يعني أنها أبطأ في جميع الحالات. لأن المعملات ‘ألفا’ و’بيتا’ هي من تحدد سرعة التناقص. وفي هذه الحالة يتم وضع ‘بيتا’ تحكيميًا.
الخطوتين السابقتين، الأولى والثانية، تمثلان ما أطلقنا عليه سابقا بجدولة التلدين.
الخطوة الثالثة
تتمثل في تكرار الخطوة الرابعة عدد من المرات. فعند كل دورة، نستخدم دالة تناقص الحرارة التي وضعناها في الخطوة الثانية. وتتوقف هذه العقدة، أي الدائرة المغلقة من التكرارات، عند الوصول لأحد شروط الانتهاء. منها الوصول لدرجة الحرارة الدنيا أو الوصول لحل مقبول حسب معايير استخدامنا.
الخطوة الرابعة
لكل فرد من أفراد الساكنة الحالية، أي نقطة من نقط الحلول الممكنة التي تشكل الفضاء متعدد الأبعاد الذي يعبر عن ساكنة الجيل الحالي، نقوم بإيجاد نقطة في جواره و مقارنته معها أي حساب احتمالية الانتقال بالاستعانة بالدالة p. ويمكن تحديد هذه النقطة المجاورة بعدد من الطرق المختلفة، على سبيل المثال، وبما أن كل حل عبارة عن نقطة في فضاء نقوم بتغيير بقيمة معينة أحد قيم إحداثياتها لإنشاء نقطة أخرى. أو عشوائيًا بزيادة أو نقص عدد من قيم الإحداثيات في أن واحد، إلخ.
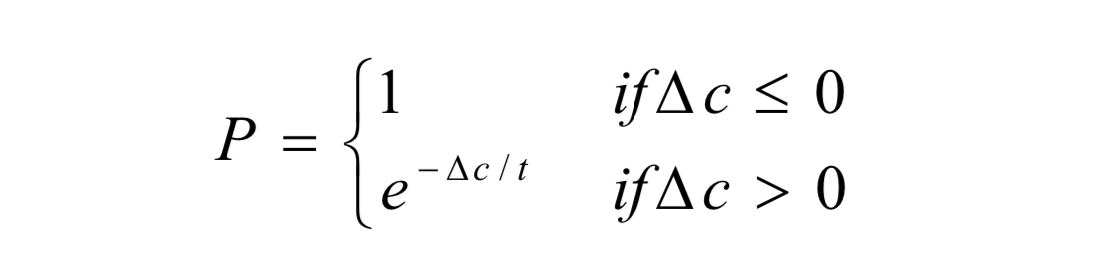
و Δc هي الفرق ببن الحل الحالي والجديد.
الحل الأقل قيمة هو الأفضل هنا وليس العكس، لكوننا نبحث عن النقطة الدنيا. يجدر الذكر أنه ليس هنالك فرق بين إيجاد القيمة الدنيا والقيمة القصوى. لأنه لو أردنا إيجاد القيمة القصوى يكفي دراسة f- بدلًا من f.
أهمية درجة الحرارة
نظرا لكيفية حسابنا للاحتمالية p، نجد أنه من المرجح إختيار حل أسوء من الحل الحالي عندما تكون درجة الحرارة مرتفعة. الشيء الذي يشكل فرقًا حاسمًا في قدرتنا على “استكشاف exploration” فضاء الحلول، ما يعزز من حظوظنا في الوصول للحل الأمثل.
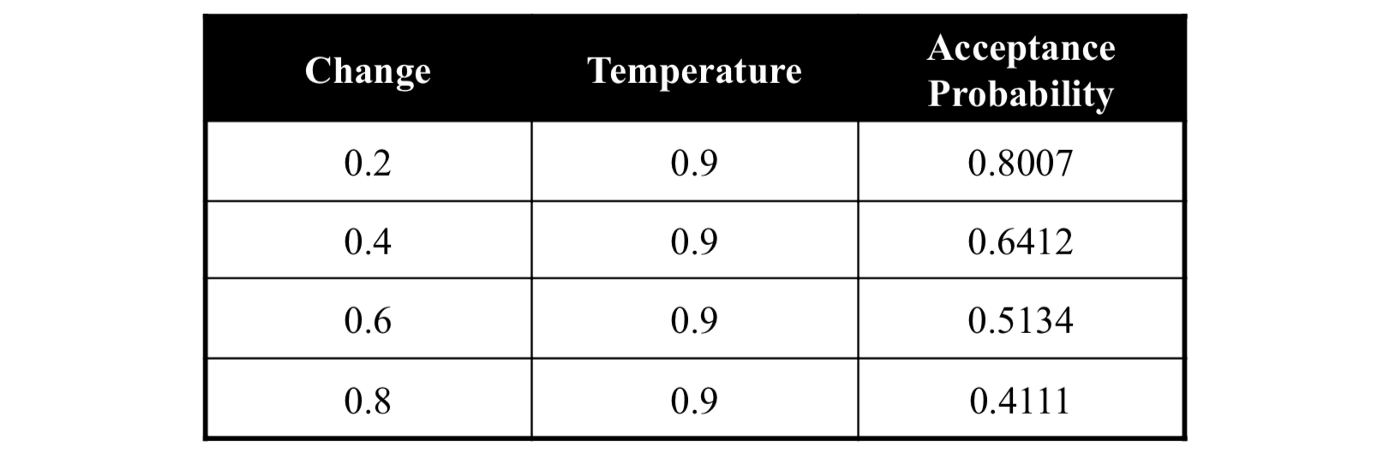
change الفرق بين ملائمة الحلين .acceptance probability نتيجة الدالة p .درجة الحرارة temperature.
عندما تكون درجة الحرارة منخفضة تقل احتمالية قبول الخوارزمية لحل أسوء أو قد لا تقبل إطلاقا أي حل أسوء. الشيء الذي يعزز بشكل كبير قدرتنا على “استغلال exploit ” فضاء البحث. فعند وصولنا للمكان الصحيح، لا داعي للبحث أكثر في أماكن أخرى. وبالتالي يجب التركيز على الموقع الحالي ومحاولة التقارب و إيجاد الحل الأمثل.
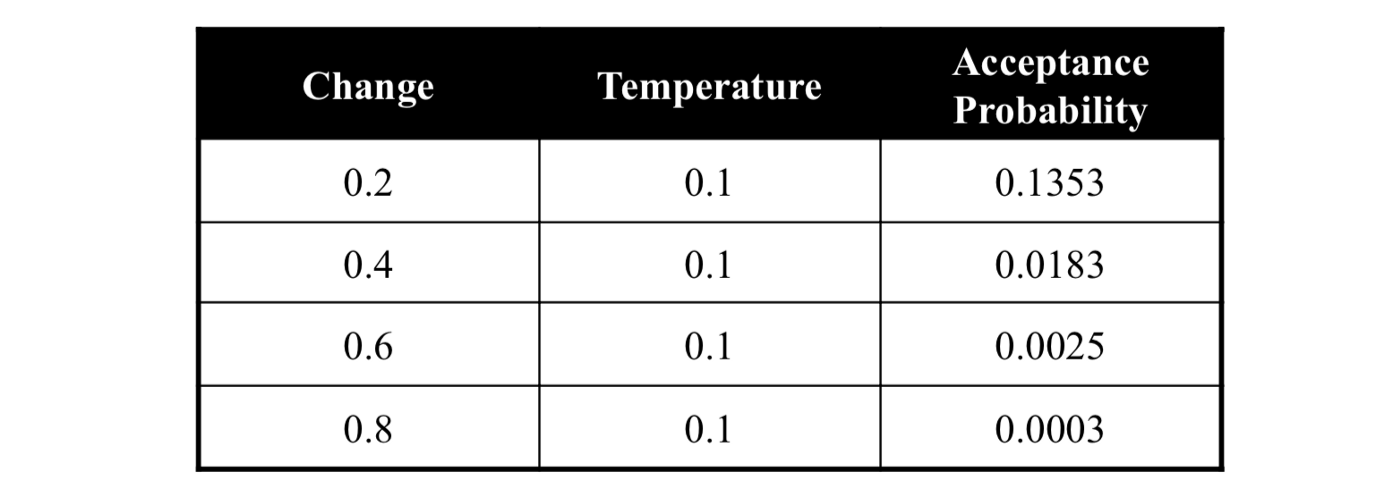
change الفرق بين ملائمة الحلين .acceptance probability نتيجة الدالة p .درجة الحرارة temperature.
هنا نلحظ أهمية تغير درجة الحرارة وأهمية سرعة ودرجة التغير على مر التكرارت في الوصول للحل الأمثل وليس فقط حلول مقبولة.
أمثلة استخدمت فيها خوارزميات التلدين المحاكى
- مشكل البائع المتجول.
- جدولة استعمال الزمن.
- مشكلة توزيع المهام.
- تقسيم وتلوين المنحنيات.
- تحسين الدوال الغير خطية.
مميزات وعيوب خوارزميات التلدين المحاكى
مميزات
- سهلة الاستخدام.
- توفر حلولا مثلى لعدد من المشاكل.
عيوب
- يمكن أن يطول أمد التنفيد إن كانت جدولة التخمير طويلة جدا.
- يوجد العديد من المعلمات والمتغيرات التي يجب دراستها، لإيجاد أفضلها لحل، كل مشكل، مثل درجة الحرارة البدئية المثلى لحل مشكل معين.
مصادر
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.




التعليقات :