- ما هي الخوارزميات المستوحاة من الطبيعة واستخداماتها ؟
- الساكنة البدئية في الخوارزمية التحسينية وأهميتها؟
- كيف يتم اختيار الخوارزميات التحسينية ؟
- ما هي الخوارزميات الجينية؟
- تعرف على خوارزمية النزول التدرجي الأشهر في الخوارزميات التحسينية
- ما هي خوارزميات التخمير المحاكى وكيف تعمل؟
- لم استوحت خوارزمية البحث التناغمي من الموسيقى وكيف تعمل؟
- خوارزمية التطور التفاضلي، الخوارزمية المستوحاة من نظرية التطور!
- خوارزمية الخفاش، الخوارزمية الثورية المستوحاة من البحث بالصدى
- ما هي خوارزمية مستعمرة النمل Ant Colony Algorithm وكيف تعمل؟
- خوارزميات النحل، الخوارزميات الثورية في مجال الحوسبة التحسينية
- دليلك لفهم خوارزمية أدم ADAM التحسينية الأكثر استخدامًا في التعلم العميق
الخوارزميات في جوهرها هي عبارة عن سلسلة من التعليمات البسيطة التي يمكن نهجها لتحقيق غاية ما. إذا ما بحثنا، نجد من بينها الخوارزميات العودية وإذا بحثنا بين هذه الأخيرة نجد الخوارزميات التحسينية، مثل الخوارزمية التالية والتي تستخدم لإيجاد الجذور المربعة لأي عدد حقيقي موجب:
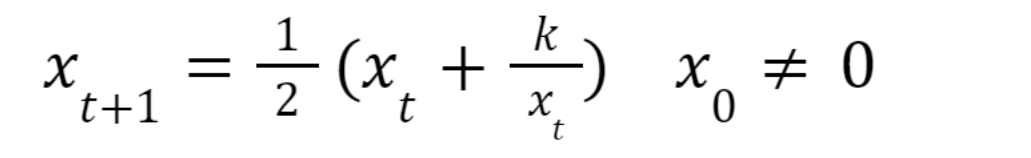
ما يحدد كفاءة الخوارزمية هو سرعة تقاربها convergence speed. ومن السهل إثبات صحة أن الجذور المربعة لأي عدد أولي هي أعداد غير كسرية، أي أنها أعداد برقم لا نهائي من الأعداد بعد الفاصلة، وبالتالي لا يمكن حسابها. لكن باستخدام هذه الخوارزمية يمكننا التقارب لإيجاد حل مرضٍ بالدقة التي نريد.
ورغم فعالية الخوارزميات التحسينية إلا أن انتاجها لا يمكن أن يتم إلا بالمحاولة والخطأ. ما يجعل إنتاجها صعبا للغاية ومستحيلًا في بعض الأحيان. ومن هنا يأتي ما اعتدنا عليه منذ الأزل وهو تأملنا الطبيعة واستنباط المنطق وراء أنظمتها لإنتاج خوارزميات جد فعالة لحل عدد لا يحصى من المشاكل. يدعى هذا الحل السحري بالخوارزميات التحسينية المستوحاة من الطبيعة.
فما هي الخوارزميات المستوحاة من الطبيعة؟ و كيف ظهرت؟ وما أبرزها؟ ما هي استعمالاتها؟ وما الخصائص التي تتشارك فيها هذه الخوارزميات؟
محتويات المقال :
ما هي الخوارزميات التحسينية المستوحاة من الطبيعة ؟
الخوارزميات التحسينية المستوحاة من الطبيعة هي مجموعة من الخوارزميات المستنبطة من الظواهر الطبيعية مثل ذكاء السرب، والأنظمة البيولوجية، والتطور الطبيعي، والأنظمة الفيزيائية والكيميائية، إلخ. ويعتبر تطوير هذه الخوارزميات فرعًا مهمًا من فروع الذكاء الاصطناعي، بحيث عرفت تطورًا سريعًا وإقبالًا واسعًا في الثلاثين عام الأخيرة نظرًا لإمكانياتها وتعدد مجالات استعمالها.
ظهور الخوارزميات التحسينية
ظهرت الخوارزميات التحسينية في بداية القرن التاسع عشر على يد عدد من علماء الرياضيات «ك ويستراس K.T.W Weierstrass»، و«شتاينر J. Steiner»، و«هاميلتون W.R.Hamilton»، و«جاكوبي C.G.J Jacobi».
ظهور الخوارزميات التحسينية المستوحاة من الطبيعة
على مر التاريخ وخصوصًا في الفترات الأولى، اعتمدت مقاربتنا نحن البشر في حل المشاكل التي نواجهها ولا تزال على التجربة والخطأ. أي أنها مقاربة تفاعل مع النظام المراد استكشافه خطوة بخطوة metaheuristic approach. فعدد كبير من الاكتشافات تم عن طريق التفكير خارج الصندوق أو بالصدفة، وهذا ما يعنيه الحدس heuristic. ورغم ذلك نجد أن أول استعمال مسجل لاستخدام هذه المقاربة كطريقة علمية رياضية meta-heuristic method لحل المشاكل problem-solving كان على الأرجح خلال فترة الحرب العالمية الثانية على يد عالم الرياضيات والحوسبة الغني عن التعريف «ألان تورنغ». استخدم تورنغ تلك التقنيات لفك تشفير إتصالات الألمان وكسر آلية تشفيرها Enigma. ورغم كون هذه الطريقة غير مضمونة الوصول للنتائج المرجوة إلا أن استعمالها في مشروعه كان نجاحًا باهرًا، ما أعطى دول الحلفاء ورقة رابحة لإنهاء الحرب لصالحهم.
بعدها بسنوات عديدة، وبدءاً من ستينيات القرن الماضي، عاد انتباه الأوساط العلمية لهذه المقاربة بتقديم عدد من الخوارزميات الثورية في مجال التحسين والحساب المعقد. حيث بدأت في هذه الفترة أول الخوارزميات التطورية بالظهور. وفي سنة 1960، اقترح مهندس الطيران حينها «لورانس جيروم فوغل» استخدام التطور المحاكى كعملية تعلم لتطوير ودراسة الذكاء الاصطناعي.
في نفس الوقت، كان العالم والمهندس «جون هولاند John Holland» يعمل رفقة زملائه في جامعة ميشيغان على استكشاف وإنتاج أول الخوارزميات الجينية. وهو ما توج لاحقًا بنشر مجموع أبحاثه في كتابه «Adaptation in natural and artificial systems» سنة 1975. بعدها تم كتابة مئات الكتب وآلاف المقالات عن هذا الموضوع.
الأعوام التي تلت كانت جد حافلة بحيث شهدت تطوير مختلف أنواع الخوارزميات وفتح مجالات بحثية خاصة بكل منها.قاد ذلك الحراك عدد من الرواد مثل عالم الرياضيات «شين شي يانغ Xin-She Yang» مطور خوارزميات مثل «بحث الوقواق CS»، و«خوارزمية الخفاش BA»، و«خوارزمية اليراعة FA»، وغيرهم.
أمثلة على الخوارزميات المستوحاة من الطبيعة
حتى الآن، تم تقديم عدد كبير من الخوارزميات المستنبطة من الطبيعة، رفقة عدد أكبر من متحوراتها الأكثر تخصصًا. يمكن لهذه الخوارزميات أن تستخدم في مختلف المجالات، من بينها نجد:
- الخوارزميات الجينية أو Genetic Algorithms، إختصارًا GA.
- خوارزميات إستمثال عناصر السرب أو Particle Swarm Optimization، اختصارًا PSO Algorithms.
- خوارزمية التطور التافضلي Differential evolution، اختصار DE Algorithm.
- الخوارزمية مستعمرة النحل الاصطناعية Artificial Bee Colony، اختصارًا ABC Algorithm.
- خوارزمية التحسين مستعمرة النمل Ant Colony Optimization، اختصارًا ACO Algorithm.
- الخوارزمية بحث الوقواق Cuckoo Search، اختصارًا CS Algorithm.
- خوارزمية الخفاش Bat Algorithm، اختصارًا BA.
- خوارزمية اليراعة Firefly Algorithm، اختصارًا FA.
- الخوارزمية المنيعة Immune Algorithm، اختصارًا IA.
- خوارزمية التحسين الذئب الرمادي Grey Wolf Optimization، اختصارًا GWO Algorithm.
- الخوارزمية البحث التجاذبي Gravitational Search، اختصارًا GS Algorithm.
- خوارزمية البحث التناغمي Harmony Search، اختصارًا HS Algorithm.
ما الخصائص المشتركة بين الخوارزميات التحسينية المستوحاة من الطبيعة ؟
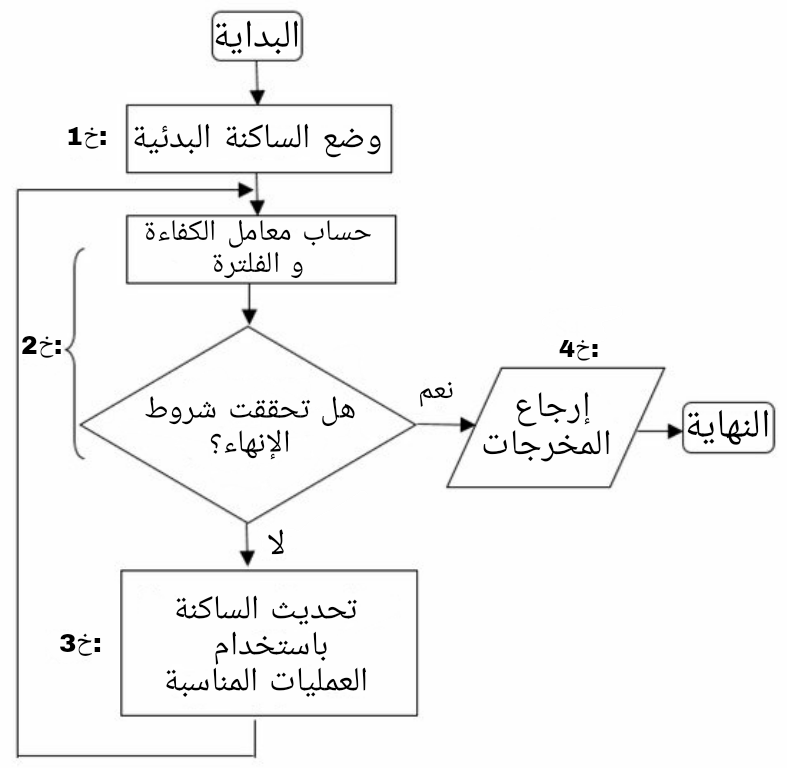
عند ملاحظة هذه الخوارزميات نجد أن لها بنية متشابهة رغم أن كل واحدة منها محددة في إطارها الخاص. من بين هذه التشابهات نجد أن المقاربة التي تنتهجها أغلب الخوارزميات التحسينية المستنبطة من الطبيعة في معالجة المشاكل التي صممت لحلها يمكن تلخيصها في أربع خطوات، وهي:
• وضع الساكنة البدئية. لتحقيق هذا، هناك العديد من المقاربات منها الاختيار العشوائي للساكنة 0، … .
في هذه الخطوة يمكننا وضع الساكنة البدئية بالحجم الذي نريد شرط ألا يتعدى السعة القصوى. بحيث أن السعة القصوى هي أقصى ما يمكن أن تعالجه الخوارزمية كمدخل بالحفاظ على سرعة تنفيذ مقبولة. وبالطبع يجب أن تكون هذه السعة أصغر بكثير من حجم مجموعة الساكنة الممكنة، لأن هذا هو المغزى وراء استعمالنا لهذه الخوارزميات.
• حساب معامل التوافق fitness value والتحقق من شروط إنهاء التنفيذ termination conditions. فإضافة إلى تحديد حجم الساكنة البدئية وكيفية بنائها، يجب أيضًا وضع المدخلات مثل المتغيرات التي تتدخل في كيفية التنفيذ وشروط وقف التنفيذ وإرجاع الحل. فأغلب الخوارزميات التحسينية تستعين بشروط للخروج من دورة التنفيذ المتمثلة في البدء، ثم المعالجة، ثم الفلترة. من بين هذه الشروط نجد:
- العدد الأقصى للتكرارات.
- العدد الأقصى للتكرارات عند عدم تغير الحل المحلي الأمثل Local Optima، أي الفرد صاحب أكبر معامل توافق أو عدد من الأفراد الأكثر توافقًا. فإن لم يتغير لعدد من التكرارات، يتم اعتباره أفضلها كحل أمثل Global Optima. أو أن التقرب للحل الأمثل غير ممكن وفي كلتا الحالتين يتم إرجاع هذا الفرد أو الساكنة الحالية ككل باعتبارها حلًا، ثم وقف التنفيذ.
- عتبة الدقة، أي نسبة الدقة التي يحق للخوارزمية عند تحققها وقف التنفيذ. وعند هذه الخطوة نقوم بفلترة الساكنة الناتجة عن الخطوة الثالثة وذلك بترتيبها أولًا حسب معامل توافقها وأخذ الأكثر توافقًا. وحجم الساكنة الذي نأخذه هنا لا يمكن أن يكون إلا أصغر من أو يساوي السعة القصوى.
- يحسب معامل الكفاءة أو التوافق fitness value باستعمال دالة نعرفها حسب الحاجة. على سبيل المثال، حساب المسافة بين النقطة والتي تليها إن كانت الساكنة عبارة عن سلسلة من النقط في فضاء متجهي وجمعها كمعامل توافق.
•تحديث الساكنة باستخدام عدد من العمليات من بينها الدمج والتحوير. فعند عدم تحقيق أي شرط من شروط الخروج، تستمر سلسلة التنفيذ ونتقدم بذلك إلى الخطوة الثالثة والتي يتم خلالها «الدمج- crossover» بشكل عشوائي بين أفراد الساكنة وإضافة الناتج إلي الساكنة الحالية. يمكن أن نفكر في هذا على أنه تزاوج وإنتاج جيل جديد يحمل صفات أسلافه. بعد هذا نقوم بنسخ الساكنة ووضع طفرات عشوائية بها random mutations ونضيفها بدورها إلي الساكنة الكلية. ونعود بعدها للخطوه الثانية.
•إرجاع المخرجات ووقف التنفيذ. فعند تحقق أحد شروط الخروج، يتم إرجاع الساكنة الحالية باعتبارها حلاً وإنهاء التنفيذ.
مفاهيم مهمة لفهم الخوارزميات المستوحاة من الطبيعة
• الطريقة «الحدسية – heuristic» هي مقاربة لحل المشاكل باستعمال طرق فعالة لكن غير مضمونة النتائج أو عقلانية في بعض الأحيان. لكن الحدسية فعالة وكافية لتحقيق المقاربة approximation وللوصول لنتائج سريعة وتحقيق أهداف متعددة على المدى القصير.
• «الأدلة العليا metaheuristic» وهي في علم الحاسوب والرياضيات إجراءات أو إرشادات عالية المستوى مصممة لإيجاد أو إبتكار أو اختيار طريقة بحث خوارزمية «حدسية» قادرة على توفير حل مقبول لمشكلة تحسينية. نلجأ إليها خاصة عند عدم توافر معلومات أو قوة حوسبية كافية تخولنا استخدام الطرق التقليدية.
أهم التحديات التي تواجه الخوارزميات المستوحاة من الطبيعة
عرفت الثلاثون سنة الأخيرة تقديم عدد كبير من خوارزميات الأدلة العليا meta-heuristic Algorithms بحيت نجد أن هذا الإنتاج متطورًا بشكل أسي أي بسرعة متضاعفة. ما جعلنا نرى في الآونة الأخيرة صدور خوارزميات الأدلة العليا بشكل يومي، وهو ما دفع بدوره تطوير الخوارزميات التحسينية والخوارزميات التحسينية المستوحاة من الطبيعة لمنحى أسي كذلك. أسهم ذلك بشكل كبير في تقديم حلول ناجحة وفعالة للمشاكل التحسينية في مجال الذكاء الاصطناعي وعدد من المجالات الهندسية الأخرى.
لكن رغم هذا التقدم الكبير و النجاح الباهر الذي حققته هذه الخوارزميات وهذا المجال البحثي، لا يزال هناك تحديات كبيرة أمامه والتي يمكن تلخيصها في أربع نقط أساسية:
• نقص البحث الكافي في النظريات البنيوية والأدوات التي تستخدمها هذه الخوارزميات مثل:
°الميكانيزمات التي تبنى عليها هذه الخوارزميات، فهي ما زالت غير واضحة أو مفهومة تمامًا حتى اليوم. ما يستدعي تعاونًا بين المطورين والعلماء المختصين في البيولوجيا والظواهر الطبيعية كون كل هذه الخوارزميات تم اقتراحها من طرف علماء حوسبة، ومهندسين.
°وضع أساس صلب من النظريات الرياضية لدعم الخوارزميات التحسينية المستنبطة من الطبيعة، مثل تحليل التعقيد الزمني time complexity، واختبار التقارب convergence proof. ومن المهم تقديم نظرية رياضية شاملة للموازنة بين التناقض بين التقارب لحل محلي convergence to a local optima وبطء التقارب slow convergence.
• نجد أن الخوارزميات التحسينية المستوحاة من الطبيعة أقل قدرة على حل المشاكل التحسينية المستمرة Continuous optimization problems في البيئات الحقيقة المعقدة. وهنا نجد أن البيئات التي نطبق عليها هذه الخوارزميات هي في الأصل معقدة، متعددة الأبعاد و الأهداف، وتهدد الدقة ومستهلكة للوقت. وفي بعض الأحيان تكون دالة تقييم الملائمة غير محددة. لذا فهذا النوع من المشاكل يشكل تحدياً كبيراً للخوارزميات التحسينية ككل رغم الجهود التي بذلت لتجاوزها.
• لا يوجد الكثير من الدراسات المشتركة inter-disciplinary researchs بينها وبين المجالات المستخدمة فيها والمجالات ذات الصلة، وذلك رغم كونها تحمل إمكانات كبيرة ذات فائدة مشتركة.
• لم يتم بذل مجهود كاف لتطبيق الخوارزميات التحسينية المستنبطة من الطبيعة في المجالات التي تستفيد منها بشكل لائق. بحيث أنها تستخدم عشوائيًا في عدد من التطبيقات دون دراسة كفاءتها لحل المشاكل ومقارنتها بالخوارزميات الأخرى فقط لكون المشرف على الدراسة قرر ذلك من تلقاء نفسه.
إمكانات خوارزميات الطبيعة
من هنا يتضح لنا أن التوجه البحثي المستقبلي في مجال الخوارزميات التحسينية يجب أن يتمحور حول معالجة هذه المشاكل؛ و ذلك بتقوية تحليل نظري متين لهذه الخوارزميات.
كما نحتاج إلى تصميم خوارزميات تحسينية أكثر تخصصًا لحل المشاكل التحسينية المعقدة، ذات الملائمة المتغيرة زمنيًا، وذات النطاق الواسع، وغيرها. كما نحتاج إلى دمج هذا المجال البحثي بمجالات أخرى. ولا يخلو هذا من فرصص دمج بتطبيقات معينة لتحسين سرعة التقارب وتحقيق أداء أفضل.
مجالات استخدام الخوارزميات التحسينية
تستخدم الخوارزميات التحسينية و بالتالي الخوارزميات المستلهمة من الطبيعة منها في عدد من المجالات للتعامل مع عدد من المشاكل العملية. ففي ظل تطور الحوسبة، أصبحت الخوارزميات التحسينية أكثر أهمية ورواجًا في عدد من المجالات الهندسية. ومن استعمالاتها نجد:
- الطرق التحسينية الكلاسيكية في الحساب Optimization methods.
- الأنظمة المعلوماتية Information systems.
- هندسة التصنيع و الأنظمة الصناعية Industrial Engineering and Manufacturing systems.
- التصميم الهندسي Engineering design.
- سلسلة الإنتاج Supply chain management.
- الفلترة الرقمية Digital filter design.
- معالجة الصور Image processing.
- تعلم الآلة Machine learning.
- تصميم المفاضلات والمكاملات الرقمية Digital integrator and differentiator design.
- التعرف على الوجوه Face recognition.
- الشبكات العصبية الاصطناعية Artificial neural networks.
وغيرها.
المصادر:
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.



شكرا لكم على هذه المعلومات.