ماذا يتبادر إلى ذهنك عند سماع كلمة (التعقيد)؟ شيء صعب، مستحيل، غير مفهوم! فالتعقيد نظرية شهيرة، إذ إن «نظرية التعقيد-Complexity theory» هي نظرية مركزية في علوم الحاسوب، إذ تستخدم نماذج حسابية مثل آلات تورنج للمساعدة في اختبار التعقيد وتساعد علماء الحاسوب على ربط المشكلات وتجميعها وإذا كان من الممكن حل مشكلة ما؛ فإنها ستفتح الطريق لحل مشكلات أخرى معقدة أيضًا ويساعد التعقيد في تحديد مدى صعوبة المشكلة وسبق لنا في مقال سابق أن تحدثنا عن الأنظمة المعقدة على نحو مبسط. لكن هل سبق وسمعت عن نظرية تسمى «التعقيد الحسابي-Computational Complexity»؟ في هذا المقال ستتعرف عليها. لما لها من أهمية عظمى، لكن بدايةً لنبدأ بنبذة عن نشأة وعلماء تلك النظرية…
محتويات المقال :
نبذة عن نشأة نظرية التعقيد الحسابي
وضعا كل من عالم الرياضيات وعالم الحاسوب «يوريس هارتمانيس-Juris Hartmanis» وعالم الحاسوب والرياضيات «ريتشارد ستيرنز Richard E. Stearns» الورقة البحثية الأساسية التي أرست أسس نظرية التعقيد الحسابي.
المحطات العلمية في حياة هارتمانيس
هاجر هارتمانيس إلى ألمانيا في نهاية الحرب العالمية الثانية، ودرس الفيزياء في جامعة فيليبش في ماربورغ قبل انتقاله للولايات المتحدة. نال درجة الماجستير في الرياضيات عام 1951 من جامعة كانساس سيتي ودكتوراه في الرياضيات 1955 من معهد كاليفورنيا للتكنولوجيا. وبدأ بالتدريس في جامعة كورنيل وجامعة ولاية أوهايو قبل أن ينضم إلى مختبر بحوث جنرال إلكتريك 1958 ومن ثم عاد إلى كورنيل لرئاسة قسم الحاسوب الجديد وتقاعد منه كأستاذ في الهندسة عام 1982. وبعد تقاعده انضم إلى مجلس العلوم في معهد سانتا في وهي مجموعة بحثية مستقلة تأسست في 1984؛ لدعم التعاون في دراسة مبادئ التعقيد.
انتُخب هارتمانس لعدة أماكن علمية مرموقة مثل:
- عضوية الجمعية الأمريكية للعلوم عام 1981.
- الأكاديمية الوطنية الأمريكية للهندسة عام 1989.
- الأكاديمية اللاتفية للعلوم عام 1990.
- أخيرًا، الأكاديمية الأمريكية للعلوم والفنون عام 1992.
إضافة إلى فوزه بميدالية بولزانو الذهبية لأكاديمية العلوم بجمهورية التشيك عام 1995 والميدالية الكبرى لإكاديمية لاتفيا للعلوم 2001 وجائزة تورينج.
المحطات العلمية في حياة ريتشارد ستيرنز
نال ستيرنز درجة البكالوريوس في الرياضيات 1958 والدكتوراه 1961 من جامعة برينستون. عمل بعد ذلك في شركة جنرال إلكتريك في المدّة ما بين 1961 و1978. وشغل منصب أستاذ في جامعة ولاية نيويورك SUNY من 1978 لـ 2000.
بالتعاون مع هارتمانيس، نشرا كتاب «حول التعقيد الحسابي للخوارزميات» في مايو 1956 وقدم ستيرنز مساهمات في تحليل الخوارزميات و«نظرية الأوتوماتا-automata theory» ونظرية الألعاب. أيضًا كتب نظرية البنية الجبرية للآلات المتسلسلة عام 1966 بالتعاون مع هارتمانيس ونظرية Compiler design مع أساتذة علوم الحاسوب بجامعة نيويورك.
الحساب والمعلومات
لنفهم نظرية التعقيد الحسابي، دعونا نبدأ بمعرفة ماهية كلمة (الحساب)، ربما الحساب بالنسبة لأغلبنا 1+1=2. وهذا أول تفسير يتبادر إلى أذهاننا وهذا مثال وليس وصفًا أو تعريفًا لتلك الكلمة. ربما نوضح هذا المثال للأطفال عند سؤالهم. فالحساب هو عملية فيزيائية محدودة بوقت ولمجموعة معينة من الدوال المختلفة. يضخم هذا التعريف من العملية الفيزيائية، ونستخدم هذا التعريف إذ إن معظم الأشياء التي تحسب تكون عادة على هيئات مجموعات. فتمثل الحسابات أيضًا معالجة للمعلومات، لكن ما المعلومات؟ المعلومات هي التي تفسر حالة نظام معين (مجموعة ثابتة من الحالات مختلفة)، فأول وصف لكمية المعلومات قدمه عالم الرياضيات الأمريكي كلاود شانون.
خصائص النظم الحسابية
بعدما تعرفنا على كل من كلمتي المعلومات والحساب المرتبطين بنظرية التعقيد الحسابي، حان الآن أن تتعرف على خصائص النظم الحسابية ومن أهم تلك الخصائص الكثيرة هي:
- القدرة المعلوماتية (أي كم الدوال في تلك النظم الحسابية ومقدار المعلومات التي يمكن تخزينها).
- السرعة (المقصود هنا سرعة معالجة النظم الحسابية لملايين البتات من البيانات في الثانية).
كما نوهنا يوجد خصائص لا حصر لها مثل الدقة وتعددية الاستخدامات وغيرها. نهاية، فالهدف من الحساب إيجاد قيم بعض الدوال.
لننتقل لفهم نظرية التعقيد الحسابي وقبلها وجب أن تكون على دراية بالمقالات السابقة في الخوارزميات وأن هنالك دوال قابلة للحساب وأخرى غير قابلة ودعونا نوضح مثال بسيط، لدينا مجموعة من الرؤوس والأضلاع وهنالك مشكلتي المساران المعروفان في نظرية الرسوم البيانية:
الأول، مسار أويلر: هو ذلك المسار الذي يمر بكل حافة مرة واحدة فقط.
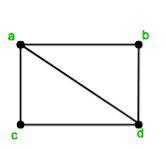
الثاني، مسار هاميلتون: المسار الذي يمر بجميع الرؤوس مرة واحدة فقط.
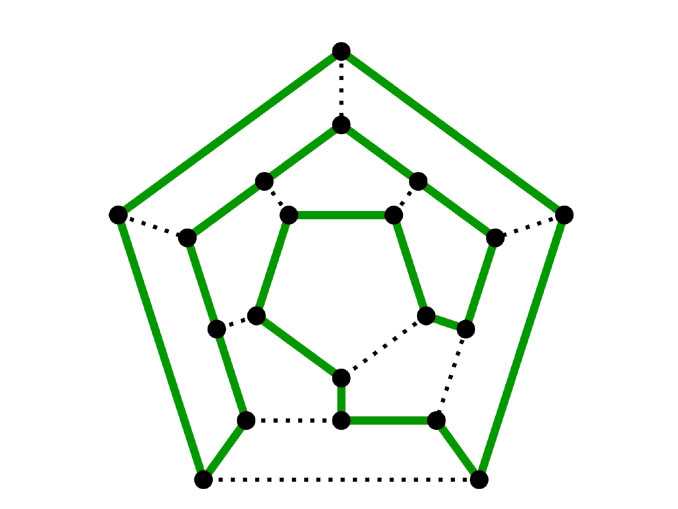
فحلل العلماء المشكلتين وأنه إذا كان لدينا خوارزمية فعالة فستحل المشكلة الأولى ولن تحل الثانية. فهنالك خوارزميات يمكنها حل مشكلات معينة وأخرى لا وذلك متعلق بقابلية الحساب وأن هنالك دوال قابلة للحساب وأخرى لا.
مثال آخر: مشكلة P وNP. إذ تمثل P مجموعة من المسائل التي لها خوارزمية حل وNP المسائل التي ليس لها خوارزمية حل؛ لذلك يمكنك معرفة المزيد من هذا المقال: ما هي حدسية P=NP؟.
نهاية عزيزي القارئ، تعد نظرية التعقيد الحسابي فرع من علوم الحاسوب وتهتم بدراسة الخوارزميات لحل المشكلات الرياضية. ومن بين أهدافها تصنيف المشكلات حسب درجة الصعوبة، أي مدى صعوبة حلها حسابيًا كمشكلتي مسار أويلر ومسار هامليتون.
المصادر
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.




التعليقات :