مدخل للمفاهيم الأساسية في الجبر الخطي وعلاقته بالحوسبة الكمية
في أواخر صيف 1949، كان الأستاذ بجامعة هارفارد «واسيلي ليونتيف-Wassily Leontief» لديه آخر الأوراق التي تحوي على معلومات حول الاقتصاد الأمريكي، إذ مثلت ملخصًا لأكثر من 250 ألف معلومة والتي أصدرها مكتب الولايات المتحدة لإحصاءات العمل بعد عامين من العمل المكثف. قسم ليونتيف الاقتصاد الأمريكي إلى 500 قطاع مثل قطاع صناعة الفحم، وصناعة السيارات، والاتصالات وهكذا… ولكل قطاع، من ثم كتب معادلة خطية وصف فيها كيف قام القطاع بتوزيع إنتاجه على قطاعات الاقتصاد الأخرى. ولأن مارك 2 أحد أكبر الحواسيب في ذلك العصر لم يستطع التعامل مع نظام من 500 معادلة في 500 مجهول، قام ليونتيف بترشيح المشكلة (وهي حل تلك المعادلات) واختزالها في نظام من 42 معادلة في 42 مجهول.
محتويات المقال :
ليونتيف والنمذجة الرياضية
تطلبت برمجة حاسوب مارك 2 جهد ضخم وكل ذلك لمعرفة المدة التي سيستغرقها الحاسوب في حل المشكلة. وها قد قام بها الحاسوب في 56 ساعة. ففتح ليونتيف الحائز على جائزة نوبل في العلوم الاقتصادية عام 1973 الباب على مصرعيه لعصر جديد في النمذجة الرياضية في الاقتصاد. إذ كانت جهوده في جامعة هارفارد عام 1949 بمثابة أول استخدام هام للحواسيب. ومنذ ذلك الوقت، استخدم الباحثون الحواسيب في المجالات الأخرى في تحليل النماذج الرياضية، وذلك يرجع إلى كمية البيانات الضخمة التي تتضمن نماذج رياضية وتكون موصوفة عادة بالمعادلات الخطية. فازدادت أهمية الجبر الخطي للتطبيقات بالتناسب مع قوة الحوسبة. إذ أدى كل جيل جديد من الأجهزة والبرامج إلى زيادة الطلب لقدرات أعلى.
فترتبط علوم الحاسوب بالجبر الخطي وهو فرع من الرياضيات يهتم بدراسة الفضاءات المتجه والتحويلات الخطية والنظم الخطية. من خلال النمو المتزايد للمعالجة المتوازية والحسابات واسعة النطاق. يعمل المهندسون الآن على حل مشاكل أكثر تعقيدًا كان يحلم بحلها قبل عقود. اليوم، الجبر الخطي من أهم المواضيع التي يجب على الطلاب في المجالات العلمية والتجارية أن يهتموا بها.
تطبيقات للجبر الخطي
سنجد الجبر الخطي في علم الوراثة وفي الاقتصاد ودراسة الأنظمة المقعدة وتحليل البيانات… كذلك هو لغة الحوسبة الكمية، فالفهم الجيد للمفاهيم الأساسية التي يُبنى عليها الجبر الخطي هام لفهم الحساب الكمي.
ومن الأمثلة الشهيرة كتطبيق له، التنقيب عن النفط مثلًا. عندما تبحث السفن عن رواسب نفطية، تحل حواسيب خاصة آلاف من المعادلات الخطية. أيضًا في الطيران، تقوم برامج خطية بجدولة الرحلات الجوية أو تخطيط الجداول الزمنية المتنوعة لخدمات الدعم مثل الصيانة. كذلك يستخدم المهندسون برامج المحاكاة لتصميم الدوائر الكهربائية والرقائق المعدنية التي تتضمن ملايين الترانزستورات فمثل تلك البرامج تعتمد على تقنيات الجبر الخطي وأنظمة المعادلات الخطية.
تعتمد ميكانيكا الكم على الجبر الخطي، إذ تستخدم النظرية العامة المتجهات اللانهائية الأبعاد. لكن لوصف الدوران والاستقطاب للكيوبت لا نحتاج سوى أبعاد محدودة مما يسهل علينا الفهم. فبعض المفاهيم الأساسية التي سنقدمها هامة فيما بعد.
سنستخدم تدوين «بول ديراك-Paul Dirac»، إذ استخدم على نطاق واسع في ميكانيكا الكم والحوسبة الكمية ولا يتم استخدامه خارج هذه التخصصات. سنستخدم الأرقام الحقيقة (الأعداد العشرية القياسية التي نعرفها جميعنا) في كتب أخرى يتم استخدام الأعداد المركبة.
لماذا الأعداد الحقيقة وليست الأعداد المركبة؟
تعد الأعداد الحقيقة سهلة الاستخدام على عكس المركبة الأكثر تعقيدًا. يعتمد النموذج الرياضي للدوران ثلاثي الأبعاد على أعدادًا مركبة، بالرغم من ذلك فالحسابات الخاصة بالكيوبتات تحتاج قياس الدوران في بعدين فقط.
سنبدأ الآن بمناقشة أهم الكميات الرياضية في الحساب الكمي وهو المتجه. إذ لفهم الحوسبة الكمية يكون للكيوبت حالات 1 أو 0 أو تراكب أو كليهما باستخدام الجبر الخطي يتم وصف حالة الكيوبت على أنه متجه ويتم تمثيله بمصفوفة. والآن لنعرف بعض المفاهيم ونبدأ بالمتجه.
ما هو المتجه؟
المتجه هو كمية لها مقدار واتجاه، وهندسيًا يمكننا تخيل المتجه كقطعة مستقيمة موجهة.
يمكننا تصور هذا المتجه كسهم ويشير في اتجاه 3 وحدات على طول المحور X و5 وحدات على طول المحور Y:

ويُمثل المتجه بمجموعة من الأرقام وهي أبعاد المتجه وإذا كانت قائمة الأرقام مكتوبة بشكل عمودي فنسيمها متجهات العمود أو كيت «ket» وإذا كانت القائمة مكتوبة بشكل أفقي تسمى متجهات الصف أو برا «bra»:
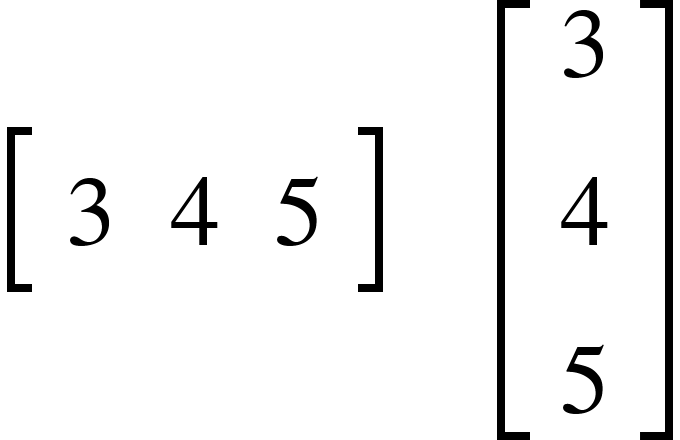
وكيت وبرا هما عبارة عن رمز براكيت، وهو رمز أدخله بول ديراك لتسهيل كتابة معادلات ميكانيكا الكم ولتوضيح الجانب المتجهي المُمثل للحالة الكمية.
الأن هيا بنا لنتعرف على العمليات الأساسية للمتجهات…
العمليات الأساسية على المتجهات
جمع المتجهات
القاعدة
(a1,b1) + (a2,b2) = (a1+a2, b1+b2)
على سبيل المثال:
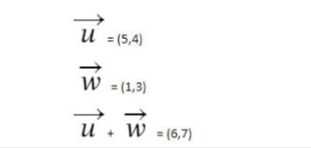
طرح المتجهات
القاعدة
(a,b) – (c,d) = (a-c, b-d)
على سبيل المثال:
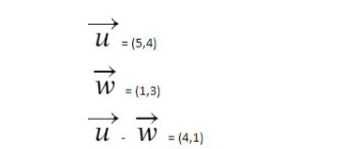
الضرب القياسي للمتجهات
القاعدة
k⋅(a,b)=(k⋅a,k⋅b)
على سبيل المثال:
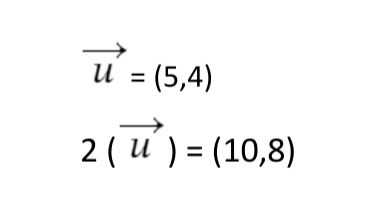
مثال شامل:
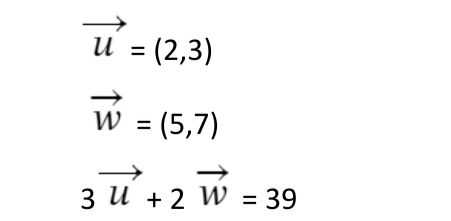
ما هي المصفوفة؟
هي ترتيب مستطيل من الأرقام وتكون مكونة من صفوف وأعمدة.
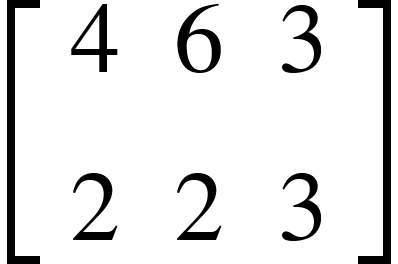
فالمصفوفة A تتكون من 3 أعمدة وصفين.
أنواع المصفوفات
مصفوفة الصف
هي مصفوفة تحوي صف واحد فقط.
على سبيل المثال:

مصفوفة العمود
هي مصفوفة تحوي عمود واحد فقط.
على سبيل المثال:

المصفوفة الصفرية
هي التي كل عناصرها صفر.
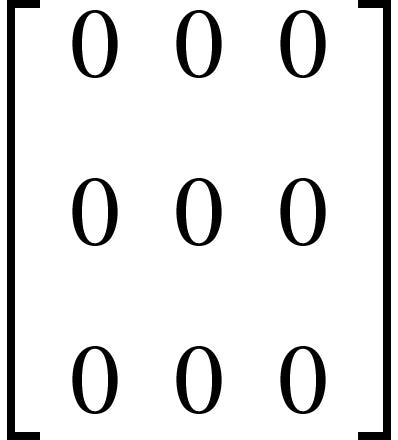
المصفوفة الأفقية
وهي مصفوفة عدد الصفوف فيها أقل من عدد الأعمدة.
على سبيل المثال:
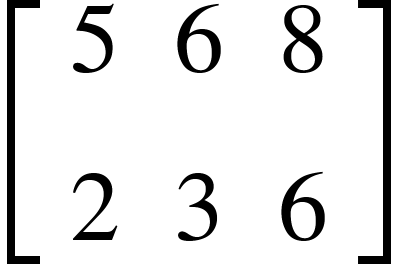
المصفوفة الرأسية
هي مصفوفة عدد الأعمدة فيها أقل من عدد الصفوف.
على سبيل المثال:
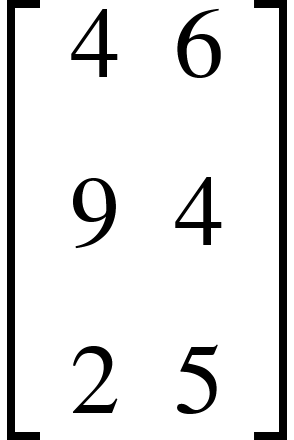
المصفوفة المربعة
هي التي عدد الصفوف فيها مساوي لعدد الأعمدة.
على سبيل المثال:
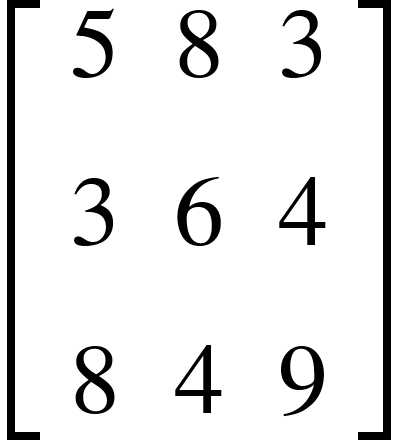
المصفوفة القطرية
هي التي يكون فيها عناصر القطر الرئيس أرقام وباقي المصفوفة أصفار.
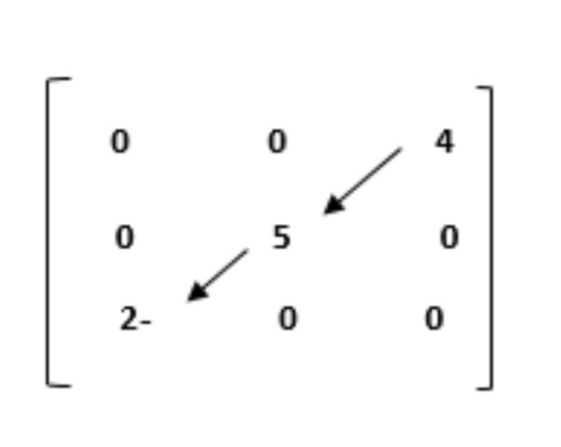
المصفوفة العددية
هي مصفوفة قطرية لكن عناصر القطر الرئيس تحتوي عدد ثابت.
على سبيل المثال:
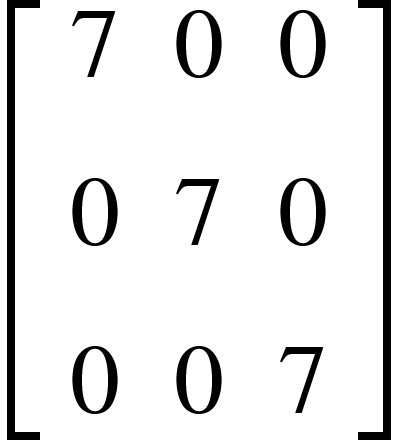
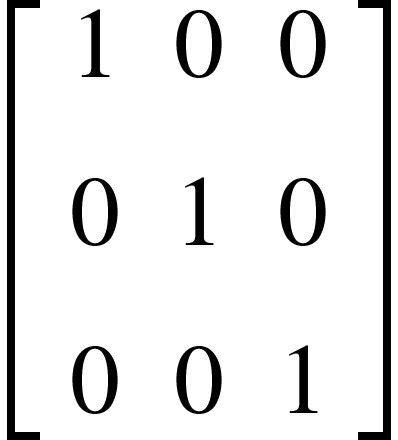
مصفوفة الوحدة
هي مصفوفة قطرية جميع عناصر القطر الرئيس تكون واحد.
على سبيل المثال:
المصفوفات المتساوية
هي المصفوفات المتساوية من حيث عناصرها.
المصفوفة المثلثية
هي مصفوفة مربعة تكون فيها العناصر أعلى أو أسفل القطر الرئيس تساوي صفر.
على سبيل المثال:

المصفوفة المفردة وغير المفردة
هي المصفوفة التي محددها يساوي صفر والمصفوفة غير المفردة هي التي محددها له قيمة غير الصفر.
على سبيل المثال:
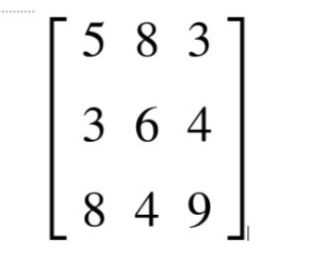
محدد المصفوفة هو أي من هذه الخيارات يعد محدد لها:
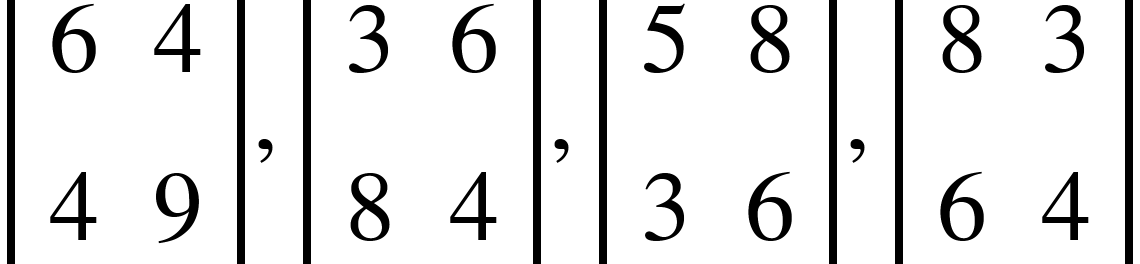
فمثلا اذا حسبنا أي محدد منهم لن يعطينا صفر فالمحدد الأول سيساوي 40 (6*9-4*4=40). لذلك المصفوفة غير مفردة.
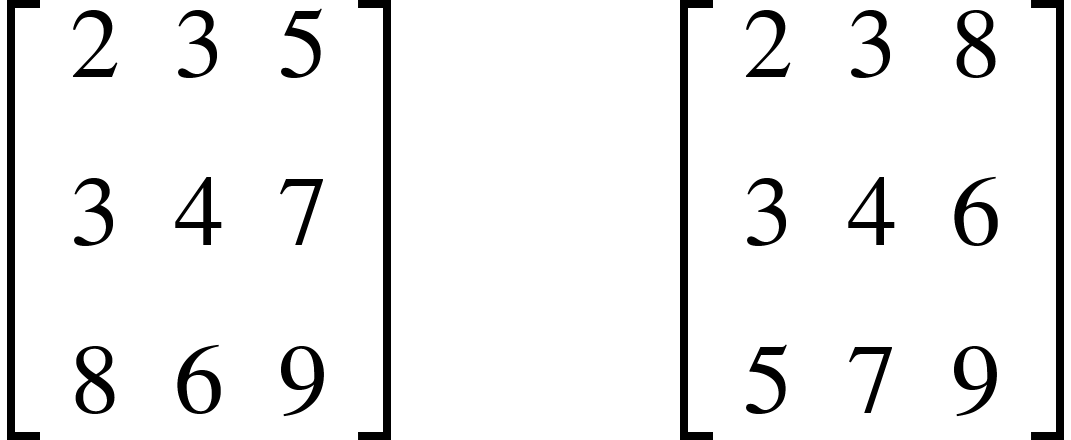
المصفوفة المتماثلة
هي مصفوفة مربعة تساوي مدورها.
على اليمين المصفوفة الأصلية وعلى اليسار مدورها:
المصفوفة شبه المتماثلة
هي مصفوفة مربعة تساوي سالب مدورها.
العمليات على المصفوفات
جمع المصفوفات
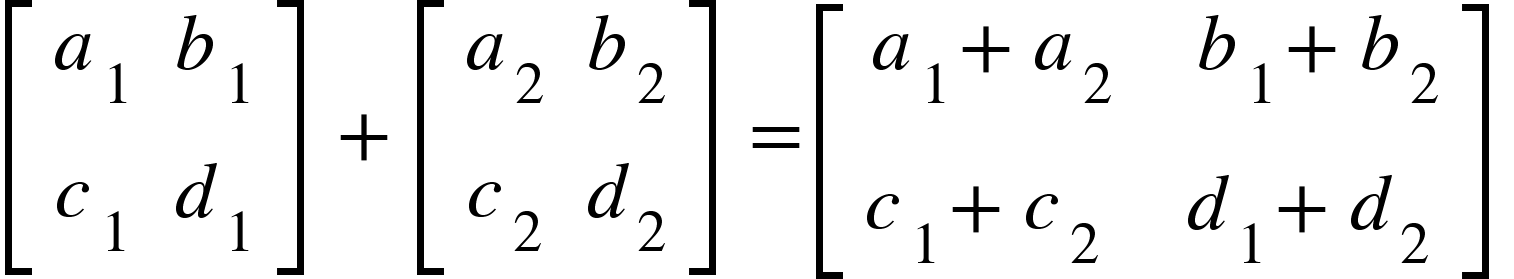
طرح المصفوفات
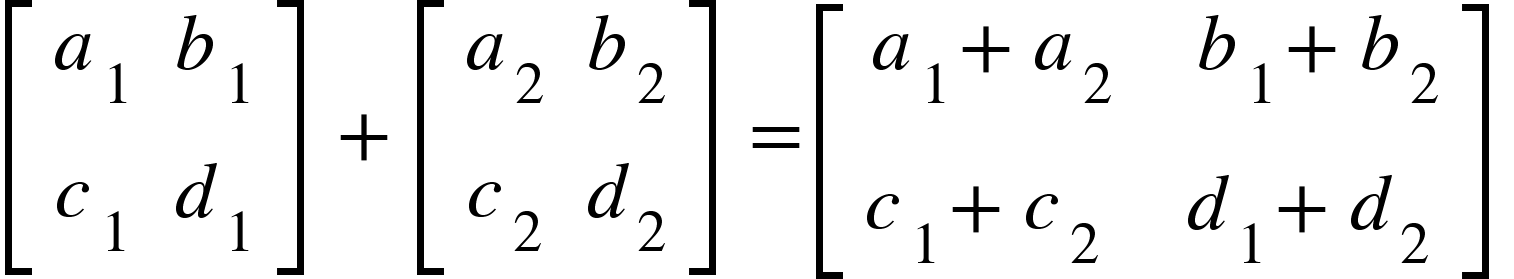
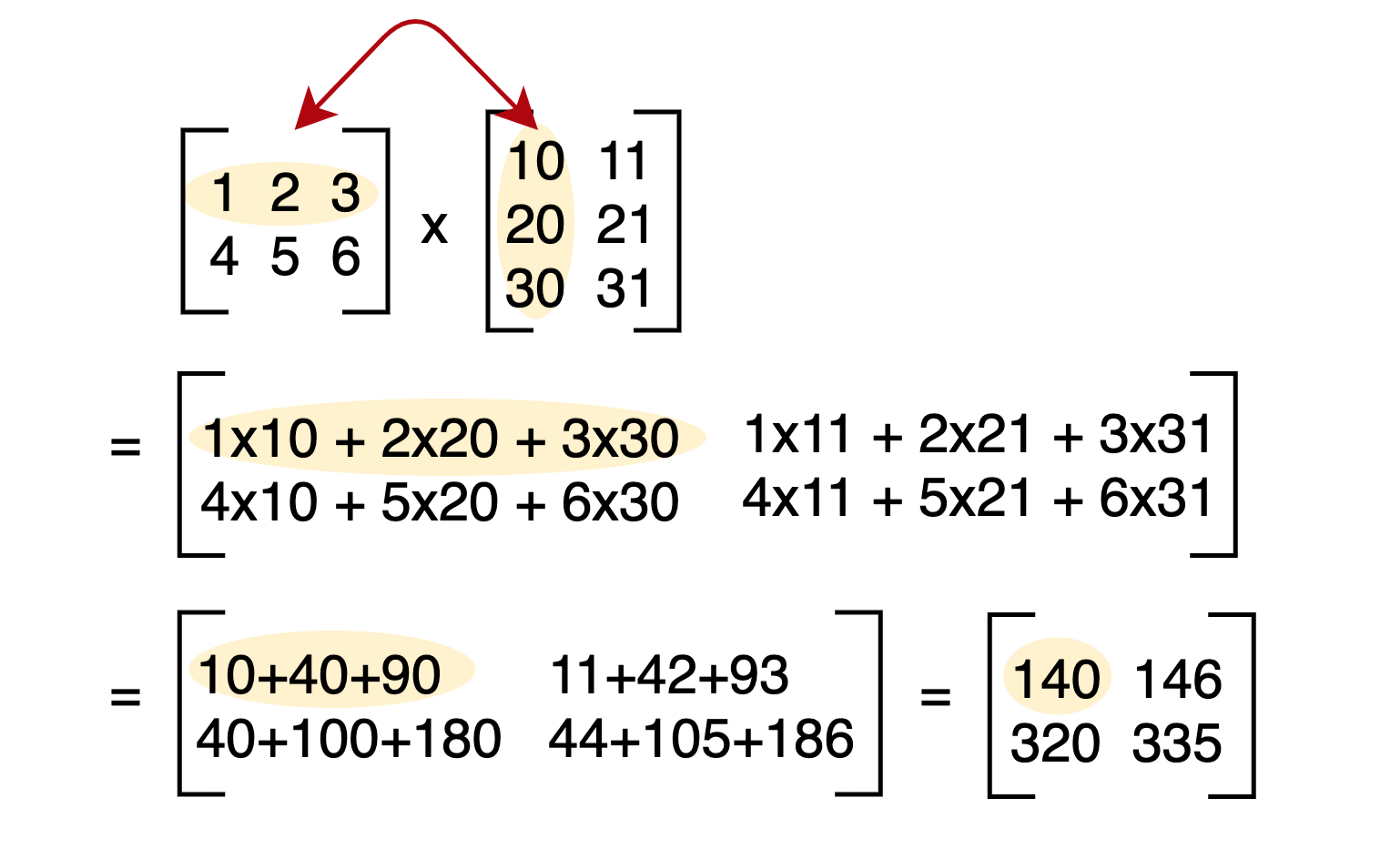
ضرب المصفوفات
لاحظ نقوم بضرب الصف الأول في العمود الثاني ونجمع والصف الثاني في العمود الثاني ونجمع وهكذا
المتجهات والمصفوفات في الحوسبة الكمية
في الحوسبة الكمية علمنا أن الكيوبت يمكن أن يكون في حالة 1 أو 0 أو تراكب أو كليهما. باستخدام الجبر الخطي، يتم وصف حالة الكيوبت على أنه متجه ويتم تمثيله بمصفوفة من عمود واحد
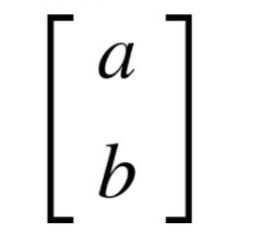
ويجب أن تستوفي حالة الكيوبت شرط
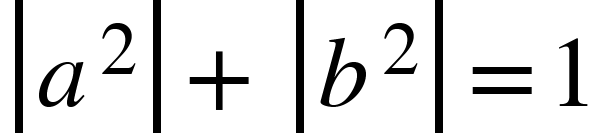
في الحواسيب والمحاكيات الكمية، تُستخدم العمليات الكمية لتعديل حالة الكيوبت. عندما يتم تطبيق عملية كمية على كيوبت، يتم ضرب المصفوفتين اللتين تمثلهما وتمثل الإجابة الناتجة الحالة الجديدة للكيوبت بعد العملية.
الأن لنأخذ مثال بسيط ونمثل حالتين لكيوبت
كل كيوبت عبارة عن فراغ متجه، لذا لا يمكن ضربه فقط. بدلاً من ذلك، يمكنك استخدام موتر (أحد الدالات الرياضية التي لا تتميز بوحدات للقياس. يتميز الموتّر بأنه يحتوي في خواصه خواص الأعداد المطلقة scalar، والمتجهات، والمعاملات الخطية)، وهي عملية ذات صلة تنشئ مساحة متجهية جديدة من مسافات متجهة فردية، ويتم تمثيلها بواسطة هذا الرمز التالي “⊗”
على سبيل المثال، حاصل الضرب الموتر لحالتين من كيوبتات:
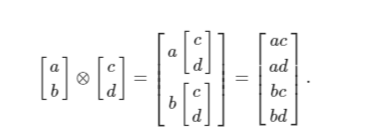
ونتيجة ذلك مصفوفة رباعية الأبعاد، إذ يمثل كل عنصر احتمالًا. في المقالات القادمة سنتعرف على المزيد من العمليات التفصيلية للكيوبت.
المصادر
- Bernhardt Chris Quantum computing for everyone-The MIT Press-2019
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.



التعليقات :