في حادثة تشيرنوبل، أدت تجربة روتينية إلى كارثة عالمية. وكان السبب في ذلك أخطاء فادحة في اتخاذ قرارات حول التحكم بالمفاعل النووي، حيث أدى قرار برفع كل أعمدة التحكم (التي تتحكم بدرجة الانشطار النووي) إلى إفلات السيطرة على التفاعلات في قلب المفاعل. فكيف يتم التحكم في المفاعلات النووية؟ وكيف نتأكد أن أحد المفاعلات لن يخرج عن السيطرة أثناء تشغيله؟
محتويات المقال :
التحكم في المفاعلات النووية
يتم التحكم في المفاعلات النووية عن طريق التحكم في «دفق النيوترونات-Neutron Flux» (كمية النيوترونات التي تخترق مساحة معينة في الثانية) داخله. ويحدث هذا بفضل قضبان التحكم التي يمكن رفعها أو تغطيسها في قلب المفاعل حسب الحاجة. فعندما نريد رفع قدرة المفاعل (كمية الكهرباء التي نريد إنتاجها) مثلًا، نرفع قضبان التحكم إلى أن نصل إلى القدرة المطلوبة ثم نعيد تغطيس جزء منها حتى لا تظل القدرة في ازدياد. وتحكم هذه العملية عدة عوامل تجعل التحكم في المفاعلات أكثر تعقيدًا مما يبدو عليه. ذاك أن التحكم في التفاعل التسلسلي الذي يحدث داخل المفاعل يستدعي حساب بعض المعاملات كمعامل التضاعف الفعال، الذي يحدد ما إذا كان المفاعل تحت السيطرة أم لا. بالإضافة إلى هذا، فإن تقادم المفاعل النووي يسمم الوقود مما يؤدي إلى تأثيرات جانبية يجب التعامل معها ضمانا لاستمرار عمل المفاعل بشكل طبيعي [1].
التفاعل التسلسلي
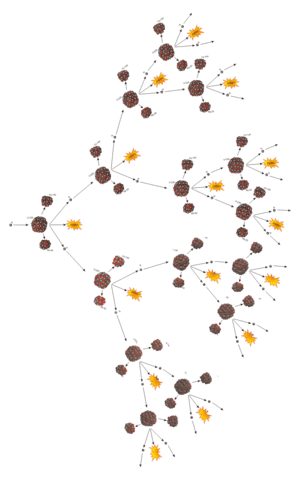
في التفاعل التسلسلي، يدخل نيوترون مقذوف في تفاعل مع نواة انشطارية فتنقسم هذه النواة باعثة معها عدة نيوترونات جديدة (بين 2 و3). وتدخل هذه النيوترونات في عمليات انشطار جديدة. وهكذا، نجد أن نيوترونًا واحدًا قد يؤدي –نظريًا- إلى عدد لا نهائي من التفاعلات (انظر الشكل 1). وهنا يأتي دور أعمدة التحكم التي تمتص جزءا من هذه النيوترونات حتى لا يخرج التفاعل عن السيطرة. ويحدد عدد الأعمدة المغطوسة بالإضافة إلى مستوى التغطيس (طول الجزء المغطوس في قلب المفاعل) نسبة النيوترونات الممتصة [1].
معامل التضاعف الفعال
يحدد معامل التضاعف الفعال keff ما إذا كان عدد النيوترونات داخل قلب المفاعل يتزايد مع الزمن. ويمثل نسبة النيوترونات المنبعثة بين جيلين من التفاعل التسلسلي، أي معدل النيوترونات المنبعثة بين انشطار والذي يليه. ويكون المفاعل في أحد من ثلاث حالات حسب قيمة Keff:
- في حالة keff < 1، يتباطئ التفاعل التسلسلي، أي أن عدد النيوترونات المنبعث يتناقص من جيل لآخر. وتوصف هذه الحالة بأنها “دون حرجة”، حيث نحاول فيها إما إيقاف المفاعل أو خفض قدرته.
- في حالة1 = keff ، يبقى عدد النيوترونات ثابتًا مع الزمن. أي أن نيوترونا واحدًا يَنتج عن عملية انشطار ما، ليُسهم في الانشطار الذي يليه. وهكذا يبقى عدد التفاعلات ثابتًا وتبقى معه قدرة المفاعل ثابتة أيضا، وهو ما يسمى بالحالة “الحرجة” للمفاعل.
- أما في حالة keff > 1، فإن التفاعل التسلسلي يتسارع، حيث يظل عدد النيوترونات يتزايد أسِّيا من جيل لآخر. وفي هذه الحالة تتزايد قدرة المفاعل فيكون في حالة “فوق حرجة”. وقد يؤدي استمرار هذا الوضع إلى خروج المفاعل عن السيطرة كما حدث في تشرينوبل.
ويمكن أن نصف حالة المفاعل بمعامل آخر هو «التفاعلية-Reactivity»، ويرمز له ب ρ. ويكتب بدلالة keff كالتالي:
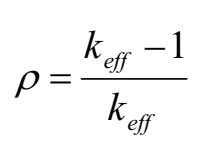
وحسب المعادلة فإن التفاعلية تكون منعدمة في الحالة الحرجة. بينما تكون موجبة في الحالة فوق الحرجة وسالبة في الحالة دون الحرجة [1]. وفي العادة، نستعمل التفاعلية في وصف تطور المفاعل وليس المعامل keff.
دورة حياة النيوترون
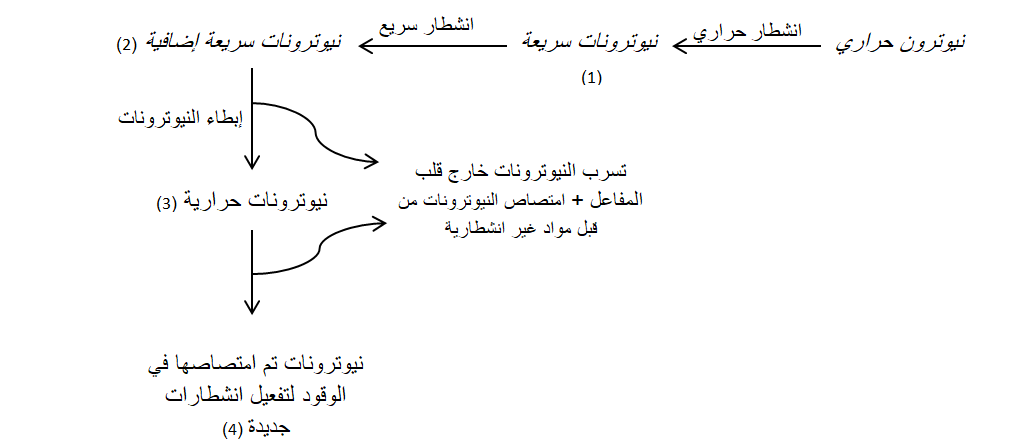
تبدأ حياة جيل من النيوترونات بانبعاثها من الانشطار النووي ثم تمر بمرحلة التباطؤ (يتم إبطاؤها حتى تصير حرارية) ومن تم تنتهي بامتصاصها في الانشطار الذي يليه. وخلال عبورها لهذه المراحل، يمكن أن تختفي بعض النوترونات وتظهر أخرى. فعند انبعاث نيوترون إثر انشطار نووي، فإنه إما يدخل في انشطار جديد فينتج جيلا جديدا من النيوترونات، أو يُفقَد من خلال امتصاصه من بعض المواد غير الانشطارية أو من خلال تسربه خارج قلب المفاعل. وهكذا، فإننا نبدأ بنيوترون حراري واحد تمتصه نواة انشطارية فينتج عنها عدة نيوترونات سريعة. تحاول هذه الأخيرة أن تتباطئ لتصير حرارية بدورها، فيُفقَد منها من فقِد عبر الشرود خارج قلب المفاعل أو عبر اقتناصه من قبل نواة غير انشطارية، ويتضاعف جزء منها بفضل الانشطار السريع -الذي ينشأ عن النيوترونات السريعة. وتشكل النسبة التي نجحت في أن تصير حرارية وتخلق انشطارًا نوويًا قيمة keff (انظر الشكل 2) [2].
صيغة العوامل الستة
تحدد «صيغة العوامل الستة-six-factor formula» قيمة keff انطلاقا من ستة عوامل متضمنة في دورة حياة النيوترون. وتكتب المعادلة على الشكل التالي:
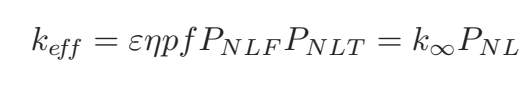
حيث يمثل η «معامل التكاثر-reproduction factor» الذي يعطي نسبة النيوترونات المنتجة بعد الانشطار الحراري (الرقم 1 في الشكل 2).

أما ε فهو «معامل الانشطار السريع-fast fission factor»، ويَحسُب نسبة النيوترونات التي أُنتِجت عن طريق الانشطارات غير الحرارية أي تلك التي حصلت أثناء عملية إبطاء النيوترونات (الرقم 2 في الشكل 2).

وبالنسبة ل p، فإنه يعبر عن احتمالية وصول النيوترونات إلى الحالة الحرارية دون أن يتم امتصاصها (الرقم 3 في الشكل 2)، ويسمى «احتمال الهروب الرنيني-resonance escape probability».
بينما يعطي «معامل الاستعمال الحراري-Thermal utilization factor f» احتمالية امتصاص النيوترونات الحرارية داخل الوقود (الرقم 4 في الشكل 2).

وأخيرا نجد PNL الذي يمثل احتمالية عدم تسرب النيوترونات خارج المفاعل. ويمكن كتابته على الشكل:
PNL = PNLT* PNLF
حيث يمثل PNLT احتمالية عدم التسرب بالنسبة للنيوترونات الحرارية و PNLF احتمالية عدم التسرب بالنسبة للنيوترونات السريعة. وتتعلق احتمالية عدم التسرب هذه بشكل المفاعل وتصميمه. ومن أجل التخلص من هذه التبعية، تم اعتماد ∞k الذي يمثل معامل التضاعف في وسط لا نهائي حيث لا وجود لأي تسربات. وهو ما يعرف أيضا ب « صيغة العوامل الأربعة- four-factor formula» [2].
ختامًا، نجد أن قيمة معامل التضاعف تلعب دورًا محوريًا في التحكم في المفاعل، حيث يتم رفع أو إنزال أعمدة التحكم حسب الحالة التي نريدها. لكن المؤسف في الأمر، أن معامل التضاعف لا يخضع فقط لمستوى إنزال أعمدة التحكم، بل إن تقادم المفاعل يسمم الوقود النووي، حيث تتراكم نواتج الانشطار النووي وتسبب تغيرات كبيرة في قيمة معامل التضاعف يجب أخذها بعين الاعتبار أثناء تشغيل المفاعل. وهذا ما سيكون موضوع المقال القادم.
المصادر
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.




التعليقات :