- ما هي الخوارزميات المستوحاة من الطبيعة واستخداماتها ؟
- الساكنة البدئية في الخوارزمية التحسينية وأهميتها؟
- كيف يتم اختيار الخوارزميات التحسينية ؟
- ما هي الخوارزميات الجينية؟
- تعرف على خوارزمية النزول التدرجي الأشهر في الخوارزميات التحسينية
- ما هي خوارزميات التخمير المحاكى وكيف تعمل؟
- لم استوحت خوارزمية البحث التناغمي من الموسيقى وكيف تعمل؟
- خوارزمية التطور التفاضلي، الخوارزمية المستوحاة من نظرية التطور!
- خوارزمية الخفاش، الخوارزمية الثورية المستوحاة من البحث بالصدى
- ما هي خوارزمية مستعمرة النمل Ant Colony Algorithm وكيف تعمل؟
- خوارزميات النحل، الخوارزميات الثورية في مجال الحوسبة التحسينية
- دليلك لفهم خوارزمية أدم ADAM التحسينية الأكثر استخدامًا في التعلم العميق
خوارزمية التطور التفاضلي أو Differential Evolution، هي مقاربة حدسية heuristic approach للتحسين الأمثل global optimization. هدفها هو إيجاد الحل الأمثل للدالة الهدف، أي القيمة الدنيا لدالة التكلفة، غير الخطية و غير القابلة للاشتقاق في فضاء البحث المعرفة فيه.
تنتمي خوارزمية التطور التفاضلي لعائلة كبيرة من خوارزميات الحوسبة التطورية evolutionary computing algorithms. فمثل عدد من طرق البحث المباشرة المعروفة، مثل الخوارزميات الجينية والاستراتيجيات التطورية، تُسْتهل خوارزمية التطور التفاضلي هي الأخرى بساكنة بدئية، من عدد من الحلول المحتملة. وبالتكرار، يتم تحسين هذه الحلول المحتملة. فتحدث طفرات وانتقاء الأصلح بين الناتج، أي الأفراد الذين يحققون أدنى قيم دالة التكلفة في محاكاة واضحة لآليات التطور البيولوجي.
تتفوق خوارزمية التطور التفاضلي على سابقاتها بقدرتها على التعامل مع المشاكل غير الخطية وغير القابلة للاشتقاق متعددة الأبعاد. ولكونها لا تتطلب إلا عدد قليل من معلمات الضبط، لتوجيه التنفيذ والحصول على نتيجة. وهذه الخصائص جعلت من الخوارزمية أكثر سهولة في التطبيق وأكثر عملية في التنفيذ.
محتويات المقال :
أصل ومقارنة
طوّر خوارزمية التطور التفاضلي كلا من رينر ستورن R. Storn و كينيث برايس K. Price بين سنتي 1996 و1997. حيث قاما بنشر مجموعة من الأوراق البحثية عنها خلال هاتين السنتين، وهو ما توجاه بعدها بكتابهما “Differential Evolution – A Simple and Efficient Heuristic for global Optimization over Continuous Spaces”، ومعناه “التطور التفاضلي: حدسية بسيطة وفعالة للتحسين الأمثل في الفضاءات المستمرة.”
وتعد خوارزمية التطور التفاضلي خوارزمية بحث تصادفية لا تستعمل المشتقات، و ذات قابلية للتنظيم الذاتي. مايجعلها مناسبة لمواجهة المشاكل ذات الدوال الهدف غير القابلة للاشتقاق. وتعتمد الخوارزمية في تنفيذها على وضع كل ما تعالجه من متغيرات وقيم على شاكلة متجهات متعددة الأبعاد وقيم عددية حقيقية. وتعالجها بواسطة عمليات مثل التقاطع crossover والتطفر mutation. وهو الشيء الذي يجعلها مشابهة لخوارزميات مثل الخوارزميات الجينية و خوارزميات البحث عن الأنماط.
ولا يقتصر هذا على تشابه فقط، إذ يمكننا اعتبار خوارزمية التطور التفاضلي بديلاً محسنًا للخوارزميات الجينية. بحيث تستعمل هذه الأخيرة معادلات محددة لتحديث الساكنة، ما يمكننا من دراسة هذه الخوارزميات دراسة نظرية.
ألية عمل خوارزمية التطور التفاضلي
معايير الفاعلية
لاعتبار خوارزمية تقليصية ما عملية يتوجب تحقيقها لعدد من الشروط، وهي:
- القدرة على التعامل مع المشاكل ذات الدوال الهدف غير القابلة للاشتقاق. والمشاكل متعددة الأطوار، أي متعددة الحلول المحلية.
- التمكن من التعامل مع الدوال الهدف المكلفة حوسبيًا computation intensive.
- سهولة الاستعمال، أي قلة وسهولة وضع معلمات الضبط.
- توافرها على خصائص تقارب جيدة، أي تماسك قدرتها على التقارب للحل الأمثل في تجارب مستقلة متوالية.
وتستمد خوارزمية التطور التفاضلي قوتها من حقيقة أنها صممت لتلبية هذه الشروط بالضبط. ما يجعلها أحد أقوى خوارزميات التحسين التطورية وأكثرها تنوعًا ضد المشاكل المستمرة.
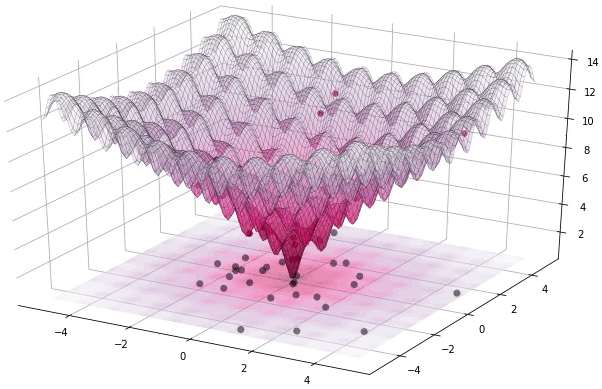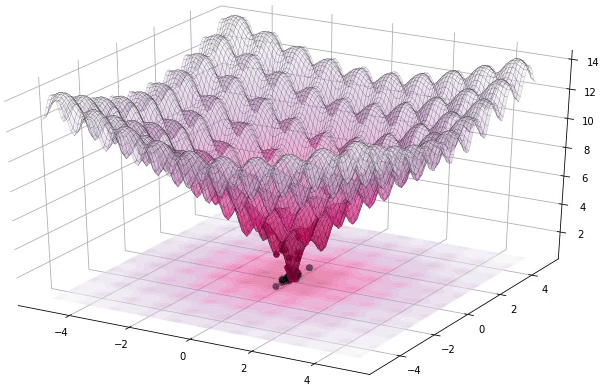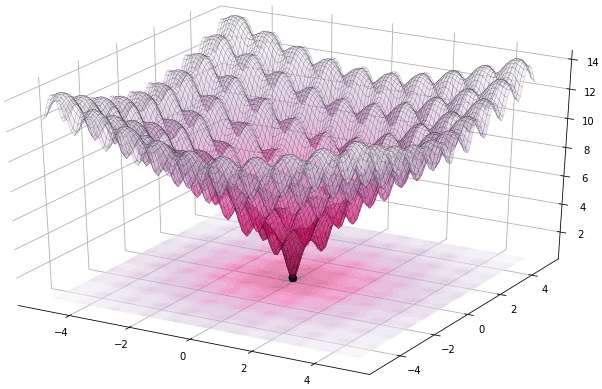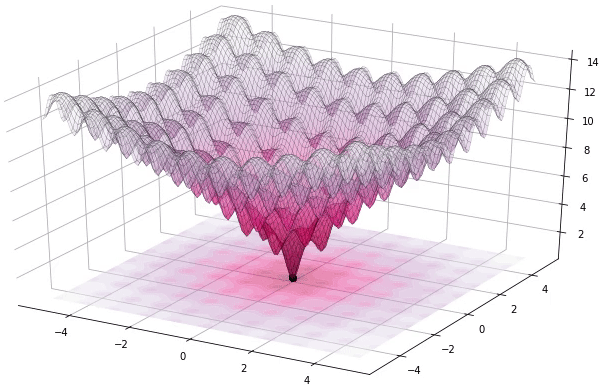
الساكنة البدئية
لمعالجة مشكل تحسيني متعدد الأبعاد، عدد أبعاده d، تقوم الخوارزمية أولا بتوليد n حل محتمل. هذه الحلول متوزعة بشكل عشوائي على فضاء البحث المدروس، و نعبر عنها بمتجهات.
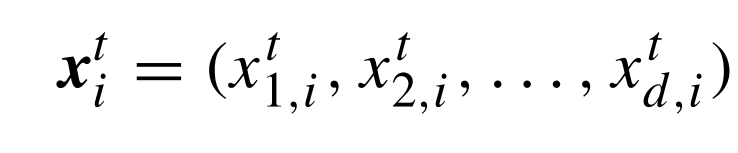
كما الخوارزميات الجينية يمكن اعتبار كل فرد من أفراد ساكنة أي جيل مجموعة من الكروموسومات أو الجينات.
العمليات الأساسية في التطور التفاضلي
نجد أن خوارزمية التطور التفاضلي تتكون من ثلاث عمليات أساسية: التطفر mutation، والتقاطع crossover، والانتقاء selection.
التطفر
يتم تنفيذ هذه العملية اعتمادًا على ما يسمى بمخطط التطفر mutation scheme. بحيث لكل متجهة Xi في أي وقت أو جيل، ونقوم باختيار ثلاث متجهات عشوائية أخرى Xp، و Xq، و Xr من نفس الجيل ونقوم بواسطتها بتوليد متجهة مانحة donor vector، كما توضح الصيغة التالية:
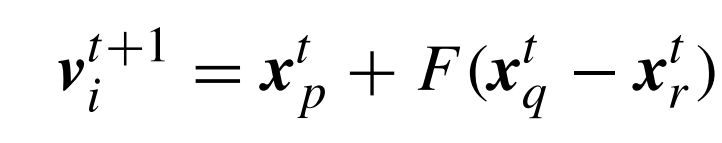
نجد أنه من الضروري توفير على الأقل على أربع أفراد ساكنة من أجل توليد المتجهة المانحة donor vector. مبدئيا نجد أن F محصورة بين 0 و 2، لكن عمليا يجب حصرها بين 0 و 1 من أجل فاعلية أعلى.
التقاطع
يُتحكم في التقاطع بواسطة المعامل Cr والذي يسمى بمعامل التقاطع. وهذا الأخير محصور بين 0 و 1. وبالتالي يتحكم في احتمالات التقاطع.
وتوجد طريقتين مختلفتين لتحقيق التقاطع. الطريقة الزوجية والطريقة الأسية.
تقوم الطريقة الزوجية على تحقيق التقاطع ببن كل أفراد ساكنة الجيل الحالي وذلك بتوليد عدد عشوائي ri محصور بين 0 و 1. هذا العدد يتحكم فيما إن كانت المتجهة الناتجة ستأخد مكون من مكونات المتجهة المانحة Vi أو المتجهة Xi، كما توضح المعادلة التالية:
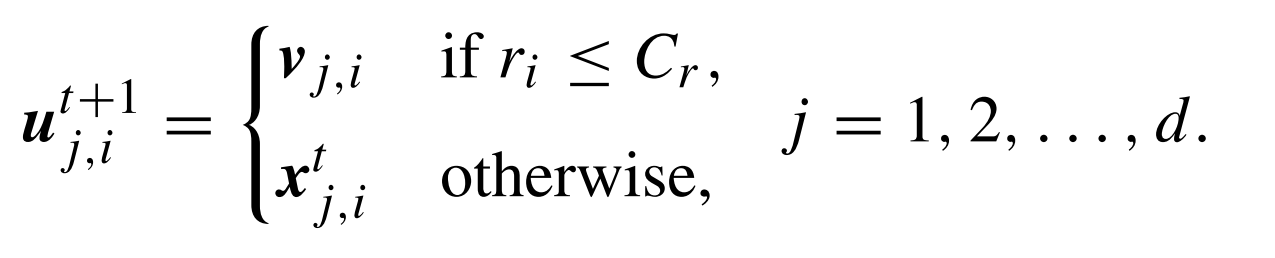
في المخطط الأسي نقوم باختيار مقطع من المتجهة يتكون من عدد من المكونات المتتالية يبدأ عشوائيًا من المكون k ويستمر إلي المكون k+L بحيث L تمثل طول هذه القطعة.
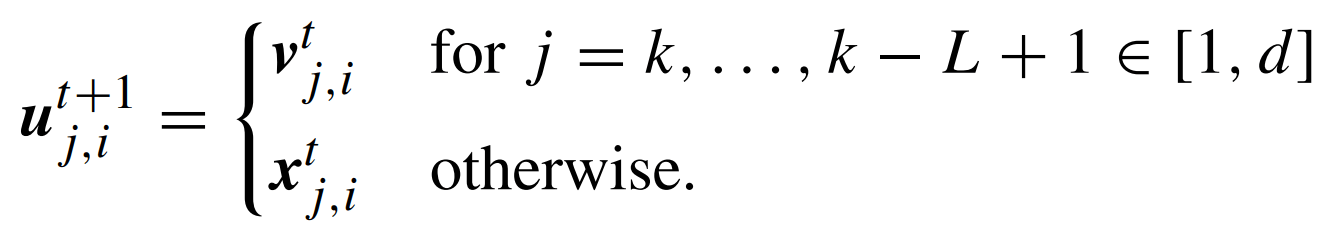
الانتقاء
تتم هذه العملية بنفس طريقة نظيرتها في الخوارزميات الجينية. بحيث يتم ببساطة اختيار الأصلح بين الفرد و خلفه، أي الفرد الذي يحقق القيمة الأدنى لدالة التكلفة بينهما، مثل ما هو موضح في الصيغة التالية:
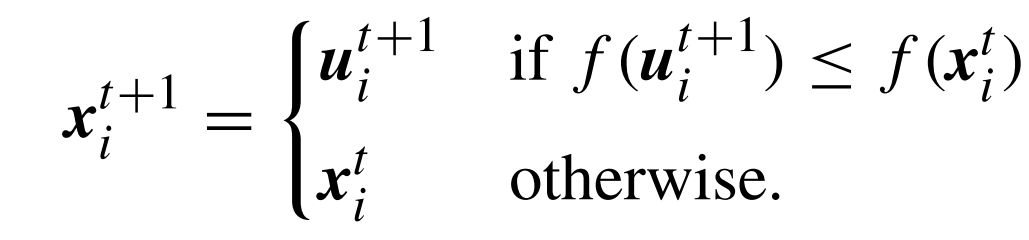
متحورات خوارزمية التطور التفاضلي
ارتكزت أغلب الدراسات على اختيار المعلمات F، و Cr، و n، وكذلك معادلة التطفر. ففي الحقيقة يمكننا توليد متجهات التطفر بطرق عديدة ومختلفة، ما يأخدنا لوضع مخططات تطفر مختلفة باصطلاح التسمية DE/x/y/z. فتمثل DE اختصارًا لاسم الخوارزمية بالإنجليزية Differential Evolution. كما تمثل x كيفية اختيارنا للمتجهة التي نحورها، ويكون هذا الاختيار إما عشوائيًا rand أو اختيار الأفضل best. وتعبر y عن عدد متجهات الفرق. و z عن خطة التقاطع إما زوجية bin أو أسية exp.
ما يعني أن */DE/Rand/1 هي الخطة الأساسية والتي تتكون من اختيار عشوائي للمتجهة التي سنحورها Rand، و متجهة فرق واحدة 1، مع مخطط زوجي أو أسي *.
بحيث تمثل DE/Rand/1/Bin معادلة التطفر:
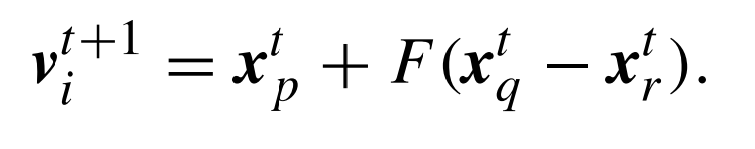
عند استبدال Xp ب Xbest نجد أن معادلة التطفر أصبحت على شكل:
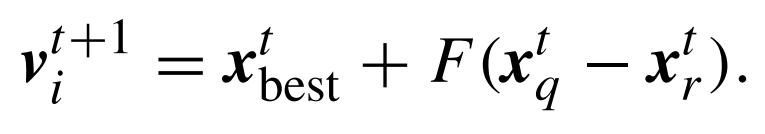
كما أنه لايوجد سبب يمنعنا من استعمال أكثر من متجهة فرق واحدة. فباستعمال متجهتين والحل الأفضل في الجيل الحالي نجد:
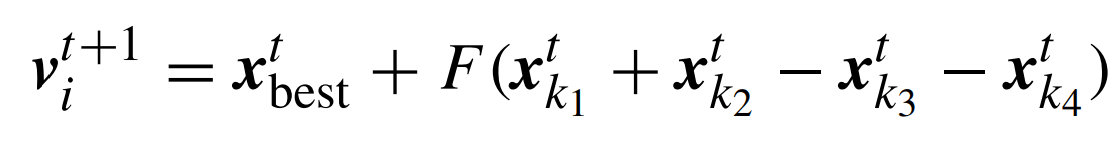
وباختيار حل عشوائي ومتجهتين نجد:
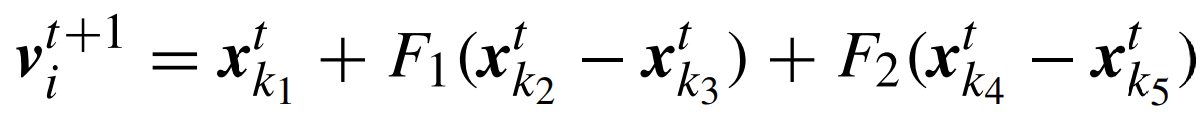
يمكننا بالطبع أخد F1 = F2 إن أردنا تبسيط المعادلة. فباتباع نفس النهج يمكن تعميم هذه المتحورات باستعمال معادلة واحدة:
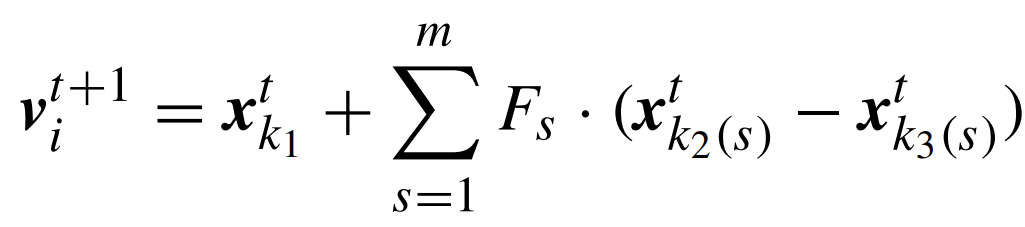
اختيار معلمات الضبط
يعتبر اختيار معلمات الضبط أمر جد مهم. بحيث أثبتت كل من الملاحظات التجريبية والدراسات البارامترية أن هذا الضبط يجب أن يتم بشكل مدروس من أجل تحقيق نتائج جيدة. ونجد أن عامل القياس F هو الأكثر حساسية، فرغم كون النظرية تتيح اختياره بين 0 و 2 نجد أن التجربة تحتم اختياره بين 0 و 1 وذلك من أجل الحصول على استقرار مناسب وكفاءة في التنفيذ. بالتجربة والخطأ تم التوصل إلي أن القيم الأفضل هي بين 0.4 و 0.95، و القيمة البدئية الملائمة هي بين 0.7 و 0.9.
يمكن اختيار معامل التقاطع Cr بين 0.1 و 0.8 مع 0.5 قيمة بدئية مناسبة. كما من الأفضل اختيار حجم الساكنة بالاعتماد على عدد أبعاد الفضاء المدروس. ففي فضاء ذو d بعد اختيار حجم ساكنة بدئي بين 5d و 10d مناسب جدا. قد يعد هذا مشكلا بالنسبة للمسائل ذات فضاءات البحث ذات أبعاد كثيرة ما يعني أنه لا مشكل في استخدام حجم ساكنة مستقل أولا من أجل اختبار الأداء.
مصادر
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.




التعليقات :