- ما هي الخوارزميات المستوحاة من الطبيعة واستخداماتها ؟
- الساكنة البدئية في الخوارزمية التحسينية وأهميتها؟
- كيف يتم اختيار الخوارزميات التحسينية ؟
- ما هي الخوارزميات الجينية؟
- تعرف على خوارزمية النزول التدرجي الأشهر في الخوارزميات التحسينية
- ما هي خوارزميات التخمير المحاكى وكيف تعمل؟
- لم استوحت خوارزمية البحث التناغمي من الموسيقى وكيف تعمل؟
- خوارزمية التطور التفاضلي، الخوارزمية المستوحاة من نظرية التطور!
- خوارزمية الخفاش، الخوارزمية الثورية المستوحاة من البحث بالصدى
- ما هي خوارزمية مستعمرة النمل Ant Colony Algorithm وكيف تعمل؟
- خوارزميات النحل، الخوارزميات الثورية في مجال الحوسبة التحسينية
- دليلك لفهم خوارزمية أدم ADAM التحسينية الأكثر استخدامًا في التعلم العميق
محتويات المقال :
أهمية وضع الساكنة البدئية
نظريًا، لتكون الخوارزمية جيدة يجب أن تكون نتيجتها مستقلة عن نقطة الانطلاق. لكن للتجربة رأي أخر، فنتيجة الخوارزميات المعتمدة على التخمين و العشوائية ترتكز بطريقة شبه كلية على نقطة الإنطلاق، أي الساكنة البدئية في حالة الخوارزميات التحسينية المستوحاة من الطبيعة.
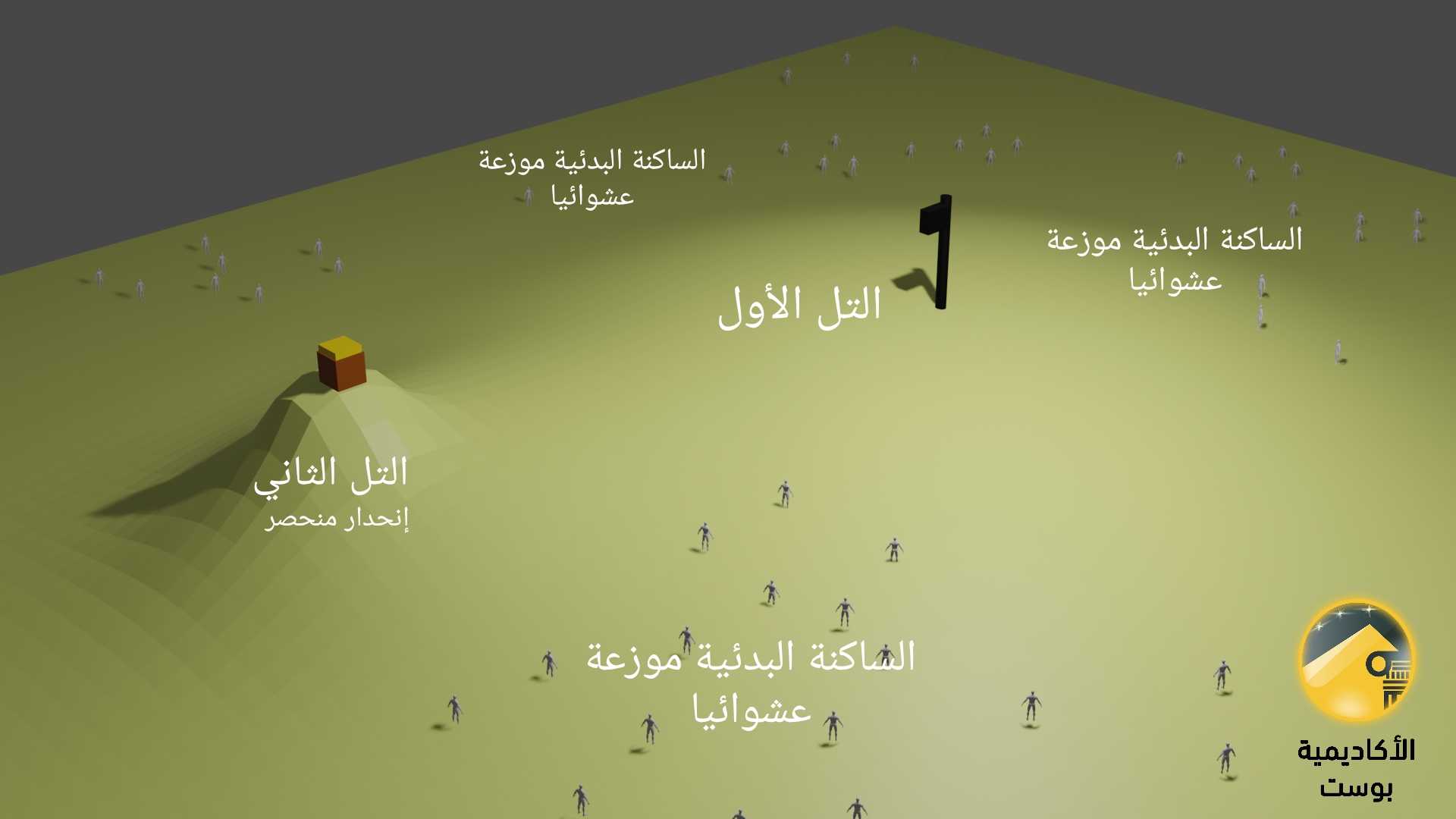
فعلى سبيل المثال، إن كان التمثيل الطبوغرافي لفضاء الحلول الممكنة عبارة عن تلين (مثنى تلال)، إحداهما متمركز في وسط الفضاء ويغطي أغلب مساحة الفضاء. والأخر منحصر في منطقة محددة داخل التل الأول، ولكن ليس في المركز. فلنسقط هذا التمثيل على أرض الواقع لنجعله لعبة إيجاد كنز، والساكنة البدئية هي اللاعبين. كل لاعب مغمض العينين، أي طريقته الوحيدة للتنقل هي الشعور بالانحدار بواسطة قدميه، ويمكنه التقدم فقط للأعلى أو للأمام إن لم يكن هناك انحدار.
كما يمكن للاعبين إعطاء تلميحات لبعضهم البعض، ولكن تلك التلميحات يمكن أن تكون صحيحة أو خاطئة. في هذه الحالة ندرك أن توزيع اللاعبين جد مهم. ذلك لأنه إن كان الكنز على قمة التل الأول فسيسير الجميع نحو قمته، نظرًا لتغطيته أغلب مساحة الفضاء وهذا جيد. لكن إن كانت أعلى نقطة في التل الثاني أي قمته هي الحل الأمثل لمشكلتنا أي مكان الكنز، فمن الصعب للغاية أن يصلها أي لاعب إن لم يكن توزيعهم ملائمًا.
الشيء الذي لا نستطيع تجنبه في أغلب المشاكل الحقيقية لكوننا غير قادرين على تمثيل فضاءات الاحتمالات ودراستها وتوزيع اللاعبين حول التل الذي يتواجد عليه الكنز. وبالتالي فأغلب اللاعبين في تلك الحالة سيتحركون نحو أعلى نقطة في التل الأول وسيتجاهلون التل الثاني لكونه منحدر وانحداره مرتكز في مساحة معينة. فإن لم يوضع أي لاعب بالقرب منه فلن يشعر أحد بانحداره.
المشاكل الحقيقية
في المشاكل الحقيقية لا يوجد تلين فقط، وتوزيع التلال يمكن أن يكون جد عشوائي وغير جيد. فمن الممكن أن يكون التل الذي يتواجد على قمته الكنز مرتكز ومتركز في أحد أركان الفضاء. ما يجعل من احتمالية وجود لاعب بقربه أمر غير مرجح، وبالتالي لن يتقدم أحد باتجاهه. هنا ندرك أن حجم وعشوائية توزيع الساكنة البدئية هي جد مهمة لوصول أحد اللاعبين للكنز، أي في الخوارزميات التحسينية تقارب أحد أفراد الساكنة بإتجاه الحل الأمثل.
يجدر الذكر أن هذه الفضاءات جد شاسعة فمحاولة استكشافها ستستهلك قوة حوسبية هائلة، لأن هذه الأخير عبارة عن فضاءات تجمع جميع الاحتمالات الممكنة. فإن لم يكن للمشكل الذي نعالجه خصائص مميزة تساعدنا في إيجاد تلميحات مرشدة لطريقة البحث فلن يختلف استكشاف الفضاء عن محاولة حل المشكل بالقوة الغاشمة أي حساب جميع الاحتمالات الممكنة ومقارنتها. كما أن الحل الأمثل ليس دائمًا هدفًا بل الهدف هو حل مقبول حسب شروط التجربة. أيضًا حجم الساكنة والتكرارات يمكنانا من التقارب وإيجاد الحل الأمثل رغم عدم وجود تلميحات تساعدنا في حل المشكل.
كيف نعالج المشاكل التي تواجهنا في وضع الساكنة البدئية؟
لعلاج المشاكل التي نواجهها في وضع الساكنة البدئية لا يسعنا إلا دراسة الخوارزمية بالمحاولة والخطأ. وذلك بتنفيذ الخوارزمية التحسينية، لحل نسخة مصغرة من المشكل لعدد من المرات باستخدام إعدادات بدئية مختلفة عند كل استعمال. الشيء الذي يخولنا لاستنتاج عدد من القيم الإحصائية مثل المتوسط والانحراف المعياري. تلك القيم الإحصائية تخولنا معرفة الإعدادات المثلى لاستخدام الخوارزمية لحل المشكل الأكبر. النسخة المصغرة هنا تعني نفس المشكل لكن بعدد مدخلات أصغر أي فضاء احتمالات صغير نستطيع التغلب عليه بالقوة الغاشمة في مدة زمنية معقولة لاستخدامه لدراسة الفعالية. كذلك يمكننا تنفيذ الخوارزمية لمدة طويلة بحيث ‘تنسى’ حالتها البدئية. الشيء الذي لا يكون ممكنًا دائمًا، وبالتالي تتقارب نحو الحل الأمثل، وذلك بطريقة مستقلة عن الساكنة البدئية. لكن مشكل هذه المقاربة هو أن سرعة التقارب تكون بطيئة للغاية. وبالتالي عدد التكرارات سيكون كبير، ما سيستهلك قوة حوسبية ضخمة.
عمليًا، نميل في استخدامنا لأغلب الخوارزميات لاستعمال المقاربة المثلى تجريبيا. والتي تساعدنا على الحصول على ساكنة بدئية موزعة بشكل جيد على مختلف نقاط فضاء الحلول الممكنة بطريقة عشوائية ومتنوعة.
كيفية تحقيق العشوائية
أحد أصعب الأجزاء في توليد الأعداد العشوائية يرجع لكون الحواسب تكرر عدد من الخطوات المبرمجة لتنفيذها، وليس لتوليد خطوات. لذا فمن المستحيل توليد شيئ لا نستطيع التنبؤ به بواسطتها.
ولهذا ننهج عدد من الطرق الإحصائية لتوليد أعداد شبه عشوائية، مثل التوزيع الطبيعي gaussian distribution، وتوزيع ليفي Lévy distribution، إلخ. يحدث ذلك بالاعتماد على أنماط عشوائية من الطبيعة والتي لا يمكن التنبؤ بها. ورغم كونها منحازة قليلاً، تبقى أفضل من نتائج الخوارزميات القطعية.
تجريبيًا، ما هي الطريقة المثلى لوضع الساكنة البدئية؟
هناك طريقتان أساسيتان معتمدتان لتوليد الساكنة البدئية المستعملة في الخوارزميات التحسينية و هما:
- الطريقة العشوائية والتي سبق وتحدثنا عنها.
- الطريقة الحدسية والتي تستعمل خوارزمية محددة لإنتاج هذه الساكنة البدئية. لكن في أغلب الأحيان يصعب إيجاد خوارزمية مناسبة، وفي أحيان أخرى يكون هذا خيارنا الوحيد.
ملاحظات تجريبية
- عند توفر خوارزميات حدسية لإنتاج ساكنة بدئية لخوارزمية المشكل الذي نريد معالجته، نجد أن استخدامها ينقص بشكل حاد من تنوع هذه الساكنة. يحدث هذا رغم عدم قدرتنا من التأكد إن كانت هذه الساكنة مناسبة للتقارب للحل الأمثل أم لا. بالتالي تحدث تضحية بالتنوع من أجل زيادة احتمال التقارب لحل، والذي يمكن ألا يكون الأمثل.
- الحلول العشوائية هي الأفضل للتقارب إلي الحل الأمثل نظرا لكون العشوائية تؤدي للتنوع في تغطية فضاء الحلول الممكنة.
نتيجة
يمكن الالتفاف على استخدام الطريقة الحدسية بعدد من الطرق عند عدم جدوى الطريقة العشوائية منها إيجاد عدد من الحلول المحتملة الجيدة بأي طريقة، واستخدامها رفقة عدد من الحلول المحتملة العشوائية لإنتاج ساكنة بدئية جيدة.
وكذلك يمكننا الدمج بين الطريقتين بحيث نقوم بوضع ساكنة عشوائية وإطعامها لخوارزميتنا التحسينية لإنتاج ساكنة جيدة. ثم نستخدمها رفقة ساكنة عشوائية أخرى كمدخل لخوارزميتنا ونعيد الكرة.
مصادر:
1- Medium
2-ScienceDirect
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.




التعليقات :