حدسية بوانكاريه هي واحدة من مسائل الألفية السبع، التي طرحها معهد كلاي عام 2000 على العالم؛ ليتحدى بها العقول الرياضية إيماناً من القائمين على المعهد بأن في الرياضيات صعوبات عميقة تتطلب جهداً وبحثاً لحلها؛ للارتقاء بالرياضيات خصوصاً وللمعرفة الإنسانية عموماً، حدسية بوانكاريه معضلة مرتبطة بفرع من فروع الرياضيات وهو الطوبولوجيا.
محتويات المقال :
ما هي الحدسية ؟
عندما يقتنع عالم الرياضيات بفرضية ما بأنها صحيحة، ولكن لا يستطيع إثباتها بالبرهان الرياضي، فإنه ينشرها على أنها حدسية، تاركاً المجال للرياضيين الآخرين من بعده لعلهم يتمكنون من إثبات صحتها.
ما هو علم الطوبولوجيا؟
فرع من فروع الرياضيات، يهتم بدراسة خصائص الأشكال عندما تطرأ عليها تغيرات في شكله دون تغير محتواه، فلو لدينا مكعب من الصلصال قمنا بتحويله إلى كرة دون استئصال أي جزء منه هنا نقول أنهما جسمان متساويان طوبولوجياً، ومن هنا نجد أن الدائرة والقطعة المستقيمة جسمان طوبولوجيان متساويان من بعد واحد، كذلك المربع والدائرة ولكن من بعدين والمكعب والكرة من ثلاث أبعاد.
ما هي حدسية بوانكاريه؟
حدسية بوانكاريه وضعت عام 1904 من قبل العالم الفرنسي هنري بوانكاريه وتنص على أن كل تنوع هندسي في أبعاد مغلقة بدون ثغرات يمكن تحويله إلى شكل كروي أي أن الشكل الكروي ذا الأبعاد الثلاثة هو الوحيد هندسياً الذي لا يتضمن ثغرات؛ ولأننا لا يمكننا تصور الأشكال في فضاء رباعي الأبعاد أو خماسي الأبعاد …إلخ فقد تسائل بوانكاريه هل يمكن تمييز السطوح ثلاثية الأبعاد بواسطة مقاييس يخضع لها الشكل ووجد بوانكاريه الاختبار الصحيح لذلك هو الاتصال البسيط.
اختبار الاتصال البسيط
اختبار يقول به شخص وهمي لا يمكن رؤيته حيث ينتقل هذا الكائن من نقطة إلى نقطة في المجسم دون أن يضطر إلى مغادرة المجسم ولفهم ذلك تأمل هذا المثال، تخيل أن هناك خيطاً مطاطي قمنا بلفه حول تفاحة، بإمكاننا لف الخيط بصورة تشمل سطح التفاحة كاملة دون أن يغادر الخيط سطح التفاحة أو أن ينقطع، وعند مرحلة ما على سطح التفاحة سنجد أن الخيط تقلص وتحول إلى نقطة، أما لو تمت التجربة على كعكعة من كعك الدونات فلن يكون هناك طريقة لانكماش الخيط ليصل إلى نقطة، لأن كعك الدونات يحتوي على ثقب.
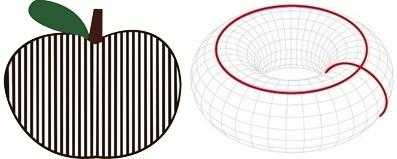
قد يبدو أن الأمر بسيطاً جداً، ولكن الصعوبة كانت في تقديم برهان رياضي مترابط ومنطقي، وكان التحدي الأكبر إثبات الحدسية في الفضاء ثلاثي الأبعاد، أما الأبعاد الأخرى فقد تم البرهنة على صحتها فالحدسية في الفراغ رباعي الأبعاد أثبتها فريدمان عام 1982، وفي الفراغ خماسي الأبعاد أثبتها زيمان عام 1961، وفي الفراغ سداسي الأبعاد أثبتها ستالينج عام 1962، وفي الفراغ سباعي الأبعاد أثبتها سمال عام 1961.
حل حدسية بوانكاريه
نجح عالم الرياضيات الروسي جريجوري ياكوفليفيش بيرلمان في 18 مارس 2010 في حل هذه الحدسية، وأقر معهد كلاي بصحة حله وأعلن عن جائزة مالية مليون دولار رفضها بيرلمان، وفي5 يونيو 2006 نشرت مجلة «اسيان اوف ما ثمتكس» وهي مجلة متخصصة في الرياضيات ومقرها الولايات المتحدة ان عالمين صينيين تمكنا من وضع الخطوات النهائية للبرهان الرياضي لحدسية بونكاريه، زاعمين أن حل بيرلمان كان معقداً وغير متكامل وما هو إلا إسهاب في نظرية تدفق ريتشي.
ما فائدة حدسية بوانكاريه على أرض الواقع؟
منحنا برهان هذه الحدسية فكرة عن شكل كوننا، وكذلك جوهر الأشكال وأصلها في الكون رباعي الأبعاد، صحيح أن إثبات الحدسية لن يؤثر على حياتنا اليومية الآن ولكن من يدري عجلة الحياة والعلم كيف تسير؟.
المصادر
1ـ Claymath
2ـ Wolfram
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.



التعليقات :