مخطط فين: نقاط التشابه والاختلاف

من المتوقع أن أغلبنا قد رأى مخطط فين من قبل حيث أنه قد ذُكر في أغلب المراحل الدراسية للتعليم من التعليم الأساسي أو المرحلة الابتدائية وحتى المرحلة الجامعية مرورًا بالمراحل المتوسطة. ومن المتوقع أيضًا أننا قد مررنا به في دراسة علوم متعددة ومنها علوم أساسية يدرسها غالبًا جميع الأشخاص مثل علوم الرياضيات. فما هو مخطط فين؟

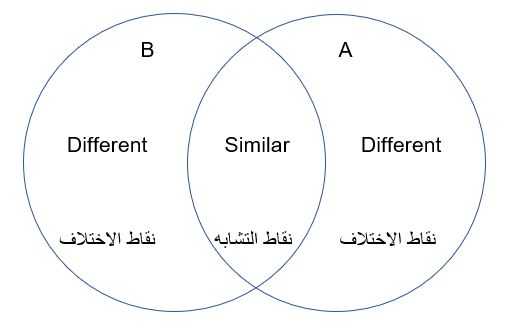
مخطط فين هو توضيح أو رسم يستخدم فيه دوائر توضح العلاقة بين مجموعة معينة ومحددة من الأشياء أو البيانات، والدوائر التي تتداخل تكون بينها عناصر مشتركة، أما الدوائر التي لا تتداخل فلا تتشارك في أي شئ فيما بينها.

تاريخ مخطط فين

تعود جذور مخطط فين إلى أكثر من 600 سنة حيث استخدم الفيلسوف وعالم المنطق << Ramon Lull – رامون لول >> نوع مشابه لهذا المخطط، وأيضًا عالم الرياضيات الألماني << Von Leibnitz – فون ليبينتز >> قد استخدم مخطط مقارب لمخطط فين الحالي.

أصبح مخطط فين جزءًا من منهج المنطق التمهيدي منذ القرن العشرين وكذلك في المرحلة الابتدائية في خطط التعليم حول العالم. وكان قد عمم عالم المنطق الانجليزي <<John venn – جون فين >> المخطط في بدايات 1800م، وسماهم دوائر أويلريان نسبة إلى عالم الرياضيات السويسري <<Leonard Euler – ليونارد إيولير >> الذي قد أنشئ مخططات مشابهة في بدايات 1700م.

لم يظهر مصطلح مخطط فين حتى عام 1918م عندما أشار الفيلسوف الأمريكي ومؤسس البراغماتية << Clarence Lewis – كلارينس لويس >> إلى التصوير الدائري لمخطط فين في كتابه مسح المنطق المركزي.

درس فين وعلّم علم المنطق والاحتمالات في جامعة كامبريدج، حيث هناك طور طريقة استخدام المخططات لشرح فروع الرياضيات ونظريات مجموعات البيانات. ونشر فين كتابه الذي كان قد كتبه سابقًا منطق الفرص والذي كتب فيه عن نظرية تكرار الاحتمالات وناقش فيه أن الاحتمالية على عكس الافتراض المشهود يجب أن تُؤسس على الانتظام والتنبؤ بشيء ما سوف يحدث.

غير العالمان << Branko Grunbaum and Henry Smith – برانكو جرونبوم وهنري سميث >> شكل المخطط إلى أن أصبح بالشكل الأسهل الذي وصل إلينا اليوم، وساعدوا على زيادة وجود مجموعات البيانات داخله. [2]

كيف نقرأ مخطط فين؟

لكي نقرأ مخطط فين بكل سهولة علينا اتباع الخطوات التالية:

1. الاطلاع على كل الدوائر التي تشكل المخطط، كل دائرة وكل البيانات داخلها.
2. الجزء من الدوائر الذي يتداخل يوضح ما هو مشترك بين الدوائر، بينما الجزء الذي لا يتداخل فهو بيانات أو عناصر فريدة للجزء الخاص به.

فوائد مخطط فين

لمخطط فين فوائد متعددة ومنها:

تنظيم المعلومات بشكل بسيط لرؤية العلاقات وما هو متشابه وما هو مختلف، ويتدرج من حجم المعلومات البسيطة إلى الأكثر تعقيدًا.

مقارنة اختيارين أو أكثر ورؤية ما هو مشترك بينهم وما يميز كلًا منهما على حدة على سبيل المثال، تحديد شراء منتج هام أو خدمة.

مقارنة مجموعات البيانات وإيجاد العلاقات والتنبؤ باحتمالات أحداث معينة.

إيضاح الأسباب والمنطق للجمل والمعادلات. [1]

حالات مشهورة لاستخدام مخطط فين في مجالات مختلفة

يتداخل مخطط فين في مجالات متعددة ومنها:

• علم الرياضيات: حيث يستخدم مخطط فين بشكل شائع في المدارس لتدريس أساسيات الرياضيات مثل مجموعات البيانات والاتحاد والاختلاف بين المجموعات. وأيضًا في الرياضيات المتقدمة لحل مشاكل معقدة ودراسة فروع كاملة.
• الإحصاء والاحتمالات: يستخدم خبراء الإحصاء مخطط فين للتنبؤ باحتمالية حدث معين وهذا يرتبط بمجال التحاليل التنبؤية. ومجموعة بيانات مختلفة تُقارن لإيجاد المشترك والمختلف.
• المنطق: يساعد مخطط فين على تحديد صحة أمر ما حيث إذا كانت المقدمات أو الأساسيات صحيحة ونموذج العمل صحيح، فيجب أن يكون الاستنتاج صحيح. على سبيل المثال، لو كل الكلاب حيوانات ولدينا كلب يدعى موجو، فإن موجو كلبًا.
• علم أصل اللغات: يستخدم لدراسة وإيضاح التشابه والاختلاف بين اللغات.
• فهم القراءة: يستطيع أن يساعد المدرسون طلابهم على رسم مخططات لمقارنة وإيضاح الأفكار التي يقرأون عنها.
• علوم الكمبيوتر: يستخدم المبرمجون مخطط فين لتصوير أو تخيل لغات الكمبيوتر والتسلسلات الهرمية.
• عالم الأعمال: للمقارنة بين المنتجات والخدمات والعمليات، ومتاح أيضًا لأي شكل من أشكال المجموعات، وهي وسيلة فعالة للتواصل.

كيف تستخدم مخطط فين في حياتك اليومية؟

لمخطط فين تطبيقات متعددة في شتى مجالات الحياة، ومن الممكن أن تستخدمه في حياتك باتباع الخطوات التالية:

1. حدد هدفك، وماذا ستقارن ولماذا وهذا سيساعدك لتعريف مجموعات البيانات.
2. عصف الذهن وترتيب الأفكار والعناصر في قوائم على ورقة أو منصة معينة.
3. استخدم المخطط للمقارنة وإيضاح الاختلافات، ومن الممكن أن ترى العناصر بشكل جديد وعمل ملاحظات واقتراحات ونقاشات.

على سبيل المثال، عندما تريد شراء سيارة وأمامك سيارتين للاختيار سيارة أ وسيارة ب، فمن الممكن رسم مخطط فين يحتوي على دائرة لسيارة أ بها المميزات الخاصة بها وأخرى لدائرة ب بها المميزات الخاصة بها، وفي المنطقة المتوسطة توجد المميزات المتشابهه في السيارتين، فذلك يسهل عليك الاختيار.

مصادر

[1] Investopedia

[2] Lucid

[3] Vizzlo

Author: Hossam Gadallah

صيدلي مهتم بتحليل البيانات في تطوير مستوى الصحة، ومهتم بالتكنولوجيا والإدارة.