حدسية ريمان من أصعب مسائل الرياضيات وأقدمها. استعصت على عقول العلماء منذ صاغها عالم الرياضيات الألماني برنارد ريمان عام 1859. حتى يومنا هذا لم يستطع أحد تقديم برهان رياضي مقبول لها. كانت ثامن مسألة ضمن مسائل هيلبرت الثلاث والعشرين والتي طرحت في المؤتمر الدولي للرياضيات في باريس عام 1900. كما أنها إحدى مسائل الألفية السبع التي اختارها معهد كلاي عام 2000، ورصد لحلها مليون دولار.
حدسية ريمان هي المسألة الوحيدة المشتركة بين اللائحتين السابقتين وذاك دليل على أهميتها. لنحاول الآن الإجابة بصورة مبسطة على سؤال ما هي حدسية ريمان؟
محتويات المقال :
دالة زيتا ريمان
لفهم فرضية ريمان علينا أولاً أن نتعرف على دالة زيتا ريمان التي تحدد قيمة معينة لكل رقم عند التعويض عنه في هذه العلاقة.
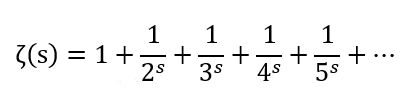
فمثلا لإيجاد قيمة الدالة عند التعويض عن s بالرقم 3 تصبح العلاقة
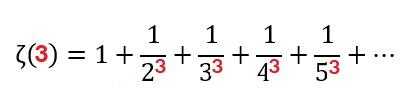
ظن ريمان في البداية أن أي قيمة أكبر من الواحد يمكننا استبدالها بـ s وتكون الدالة معرفة. لكنه لاحقاً نجح في اكتشاف أن هذه الدالة تصبح معرفة عند جميع الأعداد حتى الأعداد المركبة (الأعداد التخيلية) ما عدا الرقم واحد.
ما المطلوب لأكسب المليون دولار؟
سؤال المليون دولار في حدسية ريمان ببساطة، ما هي أصفار دالة زيتا كاملة؟، أو بمعنى آخر ما هي جميع القيم التي يمكن أن نستبدل حرف s بها وتصبح قيمة الدالة تساوي صفر، جدير بالذكر أن هناك بعض الأصفار واضحة ومثبتة رياضياً وهي مجموعة الأعداد الزوجية السالبة لكن للدالة أصفار أخرى، ابتكر ريمان افتراض طريف للمنطقة التي تقع فيها كل الأصفار الغير واضحة للدالة وهي المنطقة المحصورة بين الخط الرأسي الذي يمر بالصفر والخط الرأسي الذي يمر بالواحد وأن الأصفار الغير واضحة للدالة تقع على الخط الرأسي الذي يمر بالنقطة 0.5 ويسمى الخط الحرج
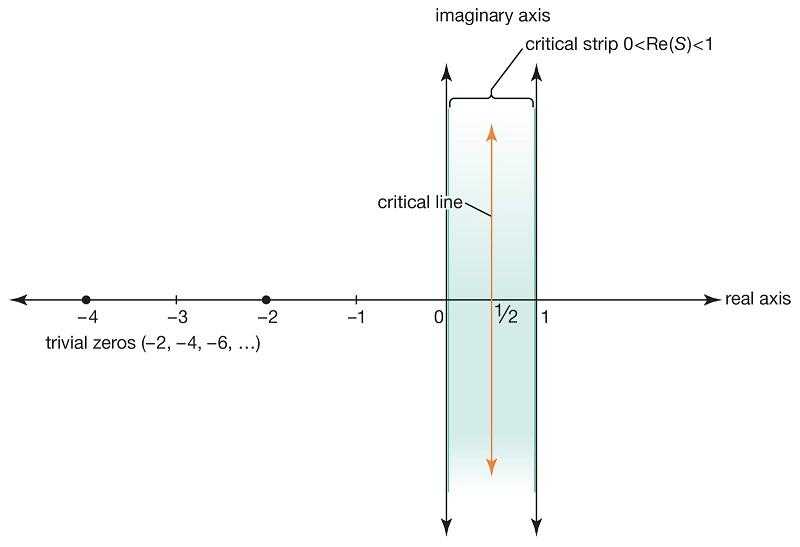
تم استخدام الحواسيب العملاقة في محاولة لتفنيد فرضية ريمان لكنها باءت بالفشل، تريليونات الأعداد تم تجربتها وكلها تؤكد على فرضية ريمان، الآن لكي تكسب مليون دولار في هذه الحدسية هناك وسيلتان، إما تقديم برهان رياضي جيد لإثبات صحة الحدسية أو تقديم عدد واحد يفند حدسية ريمان.
مايكل عطية
عالم الرياضيات البريطاني ذو الأصول اللبنانية مايكل عطية الحائز على ميدالية فيلدز وجائزة أبيل وميدالية دي مورغان، زعم أنه حل الحدسية، لكن بعد عرضه لبرهانه الرياضي في منتدى هايدلبرج لورييت، قوبل بالرفض والشك من قبل الرياضيين.
ما الفائدة من حل هذه الحدسية؟
إحدى القضايا المرتبطة بحدسية ريمان هي قضية توزيع الأعداد الأولية، فحل هذه الحدسية يعني أن يصبح لدى الرياضيين خريطة تمكنهم من تحديد مواقع الأعداد الأولية، ومن المعروف أن الأعداد الأولية هي اللبنات الأساسية لباقي الأعداد الأخرى.
المصادر:
1ـ claymath
2ـ newscientist
3ـ primes
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.


السلام عليكم .
بدون كذب شرح جميل جدا لكن عندي اسئله حول الموضوع
1ـ ما هي الصور الرسميه لداله زيتا التي تم بواسطتها وجود الاصفار(اخر صوره)
2ـ كيف تم حساب الاصفار يدويا من قبل بعض العلماء مع شرح تفصيلي