تم تسمية توازن ناش على اسم مكتشفه جون ناش، عالم الرياضيات الأمريكي. وهو يعتبر واحدًا من أهم مفاهيم نظرية اللعبة، والتي تحاول تحديد الإجراءات التي يجب على المشاركين في لعبة اتخاذها لتأمين أفضل النتائج لأنفسهم رياضيًا ومنطقيًا.
توازن ناش هو مفهوم داخل نظرية اللعبة، حيث يحقق النتيجة المُثلى للعبة ما بمراعاة خطوات وتحركات الخصم بعدد لا متناهي. حينها لا بد أن تفكر فيما سيختاره الخصم وتلعب على هذا الأساس مثلما رأينا سابقًا في لعبة قاسم أو اسرق وبالتالي يفكر الخصم فيما ستختاره، وأنت تفكر فيما سيعتقد الخصم أنك ستختاره وهكذا، إلى أن تصل لنقطة نهائية من قراءة التحركات وتعرف بتوازن ناش [2][1]. وسيتم شرح الفكرة بشكل أكبر خلال ألعاب هذا المقال. ولكن سندعوك أولًا لمشاهدة هذا المقطع من فيلم “The Princess Bride” والذي سيفيدنا في شرح الأمر بشكل ممتع.
محتويات المقال :
“مسابقة كينز للجمال – The Keynesian Beauty Contest”
في ثلاثينيات القرن العشرين، كانت مسابقة للجمال تصدر في أحد الصحف الشعبية، حيث تخمن أجمل وجه من أصل 100 صورة فوتوغرافية. يختار كل قارئ 6 وجوه، وسيتم مقارنة اختياراتهم بجميع اختيارات القُُرّاء الآخرين. إذا تضمنت اختيارات القارئ الوجه الأكثر شعبية، فسيفوز بالجائزة.

اهتمام جون كينز بمسابقة الجمال
في صباح أحد الأيام، قرأ الاقتصادي البريطاني الشهير جون ماينارد كينز عن هذه اللعبة في صحيفته المحلية. كان كينز، في ذلك الحين اقتصاديًا كبيرًا بارعًا، يكافح كثيرًا في البورصة. لذلك، أصبح مهتمًا بإيجاد نموذج يشرح سبب تذبذب أسهم البورصة وانهياراتها وغيرها من التقلبات السريعة في الأسعار، على الرغم من عدم تذبذب القيم الأساسية للأسهم من يوم إلى يوم. ألهمته لعبة مسابقة الجمال كنموذج محتمل، وشرع في الكتابة عن ذلك في عمله عام 1936 تحت عنوان “النظرية العامة للتوظيف والفائدة والمال”.
استراتيجية كينز
وفقًا لكينز، يمكنك استخدام استراتيجيات مختلفة متعددة عند لعب لعبة مسابقة الجمال. أولًا، يمكنك ببساطة اختيار الوجوه الستة التي تجدها شخصيًا أكثر جاذبية. ويطلق كينز وغيره من خبراء الاقتصاد على هذه الاستراتيجية اسم “الاستراتيجية الساذجة”، لأنها تستند إلى افتراض مفاده أن تفضيلاتك مطلقة. استراتيجية أخرى تنطوي على بناء قرارك على ما تعتقد أن اللاعبين الآخرين سيجدونه جذابًا.
ومع ذلك، فإن هذا الأمر غير مبني على الاختيار الأكثر عقلانية، فهو يعمل على افتراض أن الجميع يستخدمون الاستراتيجية الساذجة فحسب. ولكن ماذا لو استخدم الجميع الاستراتيجية الأكثر تطورًا، وحاولوا تخمين ما يجده الآخرون جذابًا؟ حسنًا، سيصبح الأمر معقدًا. ليس عليك فقط تخمين ما يجده الآخرون جذابًا؛ بل يجب عليك أن تخمن تخمينات الآخرين أيضًا. ولكن بمجرد أن نعتمد هذه الاستراتيجية، ينتهي بنا المطاف في حلقة لا نهائية تمامًا كما حدث في مقطع الفيلم بالأعلى.
حلقة لا نهائية
للمضي قدمًا، يحتاج كل لاعب إلى الذهاب لمستوى أعمق من أي شخص آخر، حيث سيصبح بحاجة إلى تخمين تفضيلات الآخرين وقراراتهم، بل وتخمينات الآخرين حول تخمينات الآخرين، وهلم جرًا. رغم أنها لعبة بسيطة لتحديد الوجوه الأكثر جمالًا إلا أن الأمر أصبح معقدًا، وتحول الأمر للعبة تخمين لا نهائية. [3]
تطبيقات نظرية كينز في البورصة
شبّه كينز هذا الشكل من التفكير الاستراتيجي بالبورصة واستراتيجيات المضاربة لكسب مال سريع. إذ يجب علىى المضارب الماهر شراء الأسهم قبل أن يشتري الجميع وبيعها قبل أن يبيع الجميع. من خلال القيام بذلك، يمكنك ركوب موجات من ثقة المستثمرين لترتفع أسهمك ثم الخروج قبل أن تتهاوى في دورتها الحتمية.
لذلك، إذا استطعت معرفة ما يفكر فيه غالبية المشاركين في سوق الأسهم، يمكنك التغلب عليهم. ومع ذلك، يحذر كين من استخدام نفس المنطق المعيب اللا نهائي الذي رأيناه في مسابقة الجمال.
إذ يحاول الجميع تخمين ما سيشتريه ويبيعه المستثمرون الآخرون، وما سيخمنه المستثمرون الآخرون عن المستثمرين الآخرين؛ وهلم جرًا إلى الأبد. من الممكن أن تفوز فَوْزًا كبيرًا إذا كنت تخمن كل شيء بشكل صحيح، إلا أنك ستصبح أكثر عُرضة للخسارة. فالتخمينات عدد لا حصر له من المرات ومن الممكن أن يحمل نسبة أكبر من الأخطاء.[3]
لعبة “2/3 المتوسط”
لعبة “2/3 المتوسط” هو لغز معروف في نظرية اللعبة، ويوضح بعض المفاهيم الأساسية للنظرية. باختصار، إليك بيان المشكلة:
لنفترض أن كل شخص في بلدتك يختار رقمًا صحيحًا يتراوح بين 0 و100، كما أن 0 و 100 هما خياران محتملان ضمن المجموعة أيضًا، كما هو الحال مع أي رقم آخر بينهما. الفائز هو الذي يختار أقرب رقم إلى 2/3 من متوسط الأرقام المختارة. ما هو الرقم الذي تختاره؟ لماذا؟
لنبدأ بطريقة لطيفة لعرض المشكلة وهي البدء بتحديد مجموعة الأرقام التي لا ينبغي لأي لاعب عقلاني اختيارها. بشكل منطقي، سيشعر أغلبنا بأن الجواب الفائز لن يكون 100. لماذا؟ لأن متوسط الأرقام لا يزيد عن 100، ولا يمكن أن يكون أكبر من 100! وبالتالي، لا يمكن أن يكون 2/3 من المتوسط هو 100. لذا سيلجأ المرء إلى خيار أفضل.
في الواقع، 2/3 من متوسط الأرقام التي لا تزيد عن 100 لا يمكن أن يكون أكبر من 66.666، لذلك، فمن غير المنطقي اختيار عدد أعلى من 66.666. لذا من الأفضل اختيار عدد أقل من هذا الرقم.
إذا كنت عقلانيًا، فلن تحدد رقمًا أكبر من 66.666 بالطبع، وهذا يقودنا إلى المرحلة التالية من التحليل. هل يمكنك أن تفترض أن الجميع منطقيون؟ إذا كان الأمر كذلك فإن جميع اللاعبين قاموا باستبعاد الأرقام فوق 66.666 من اختياراتهم، وهذا يقلل من الاحتمالات لاختيار عدد بين 1 و 66.666. وفي محاولة للحصول على الأقرب إلى 2/3 من متوسط رقم 66.666 سنصل في هذا الحالة = 44.444، وتستمر هذه العملية – باعتبار جميع اللاعبين في أعمق مستوي من العقلانية والمنطقية- إلى أن يصل الرقم الفائز إلى 0 حيث يختار جميع اللاعبين 0 وهذا ما يعرف بتوازن ناش.
هل توازن ناش هو الرابح؟
حالة أن الجميع يختار صفر هو توازن ناش، تعني أنه لن يندم أحد على اختياره. والوصول إلى توازن ناش يتطلب أكثر من مجرد عقلانية ومنطقية من جانب اللاعبين. بل، يتطلب أن يفترض الجميع أن الجميع يفترض أن الجميع يفترض … أن الجميع عقلاني ومنطقي (سلسلة طويلة من التخمينات تكاد تكون بعدد كل المشاركين). وتعرف عملية التخلص المتكرر من مجموعات الأرقام التي قد يكون اختيارها غير منطقي بـ”القضاء المتكرر على استراتيجيات الهيمنة الضعيفة “.
هل تعتقد أن الخيار الفائز سيكون الصفر حقًا؟ أراهنك بلا. لأنه من غير المحتمل أن يتبع كل شخص في بلدتك سلسلة المنطق المذكورة أعلاه. قد يكون الجميع عقلانيين. وقد يفترض الجميع أن الجميع عقلانيون. قد يفترض الجميع أن الجميع يفترض أن الجميع عقلانيون. ولكن في مرحلة ما، بعض اللاعبين سيوقفون التسلسل. في الواقع، يكمل الناس هذا التسلسل إلى أربعة مستويات في المتوسط. ورقم 21.6 كان هو الرقم الفائز في مثل هذه اللعبة التي نظمتها صحيفة دنماركية مع 19196 مشاركًا.
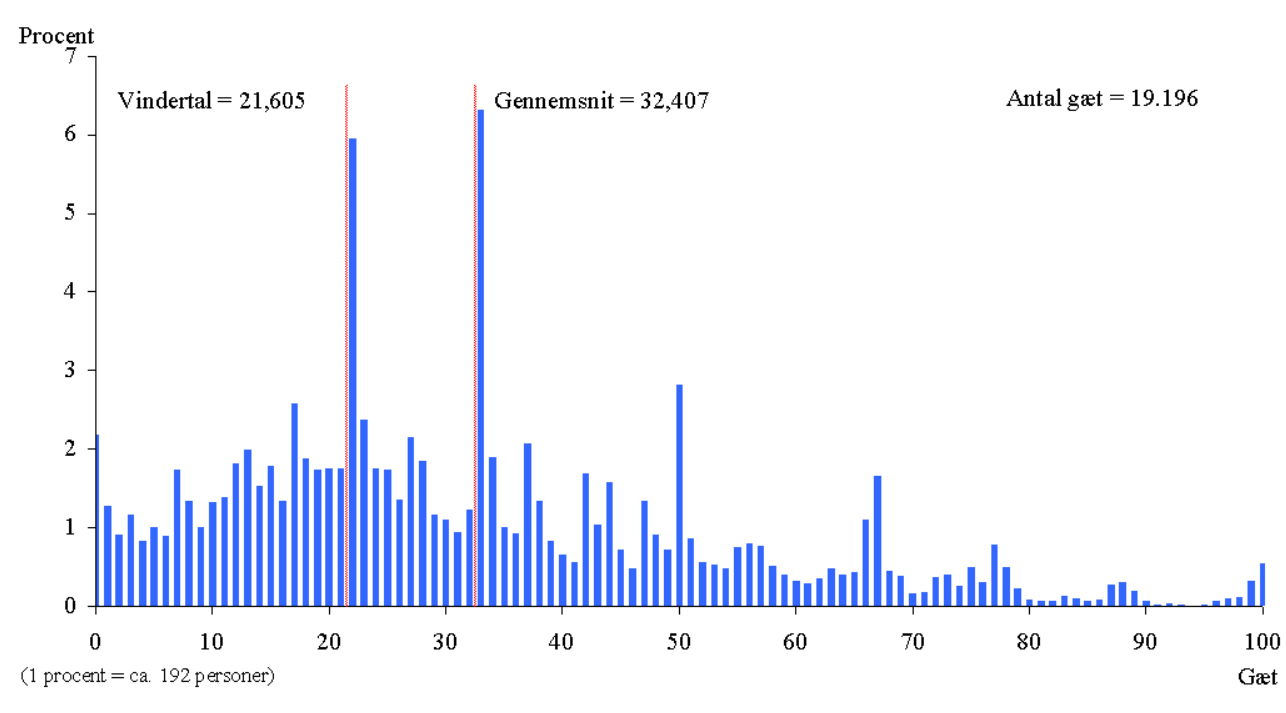
الموجز عن توازن ناش
توازن ناش هو عنصر من عناصر نظرية اللعبة وهو النقطة الذي سيقف عندها اللاعب ولا يغير قراره أو استراتيجيته حتى عند معرفة استراتيجية الخصم. فعند وصوله لتوازن ناش لن يحتاج لتغييره لأنه الأفضل للجميع ألا وهو الصفر في اللعبة الماضية. يمكن تطبيق توازن ناش في مجموعة متنوعة من المواقف الواقعية في تحديد أفضل مكافأة في السيناريو الذي سيتم استنادًا إلى قراراتك وكذلك قرارات خصمك. إلا أن توازن ناش لا يعني بالضرورة أن يصف الواقع كما رأينا، فهو لا يدرس الماضي، بل يحاول التنبؤ بالمستقبل بطريقة رياضية متسلسلة لا تضمن الفوز في جميع الحالات.
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.





التعليقات :