محتويات المقال :
مقدمة في قوانين الاحتمالات
تعود دراسة الاحتمال كفرع من الرياضيات إلى أكثر من 300 عام، إذ نشأ بسبب الأسئلة المتعلقة بألعاب الحظ مثل لعبة رمي النرد… وفي هذا المقال سنعرض مقدمة في قوانين الاحتمالات، إذ أن تعلمها هو جزء مهم لاستيعاب علوم كثيرة مثل الطب والفيزياء وعلوم الحاسوب والحوسبة الكمية وحتى في حياتنا اليومية في اتخاذنا للقرارات.
يمكنك معرفة تاريخ علم الاحتمال وأهميته من خلال هذا المقال: نظرية الاحتمال بين الماضي والمستقبل.
ما هي التجربة؟
التجربة: هي أي نشاط أو عملية، تخضع نتيجتها إلى عدم اليقين (أي أننا لسنا متأكدين من نتيجتها بنسبة 100٪). على الرغم من أن كلمة “التجربة” تُشير عامة إلى حالة اختبار معملية مخطط لها أو خاضعة للرقابة، لكن نستخدمها في علم الاحتمال على نحو أوسع.
في تجارب مثل رمي عملة معدنية مرة واحدة أو عدة مرات، واختيار بطاقة أو بطاقات من مجموعة، والتأكد من وقت التنقل من المنزل إلى العمل في صباح يوم معين، والحصول على فصائل الدم من مجموعة من الأفراد، وغيرها.
ما هو «فضاء العينة-Sample space» في التجربة؟
فضاء العينة: مجموعة من جميع النتائج المحتملة لتجربة عشوائية، تُمثل بالرمز “S”، نكتب النتائج في قوسين هكذا “{}”.
مثال: عند رمي قطعة نقود، فإن هناك نتيجتين وهما «الرأس والذيل (صورة وكتابة)-Head and Tail»، إذًا فإن فضاء العينة لتلك التجربة سيكون:
S = {H,T}= {Head, Tail}.
وعند رمي العملة مرتين، سيكون عدد النتائج المحتملة أربعة. سنفرض أنهم H1, T1 للمرة الأولى وH2 وT2 للمرة الثانية، فيكون فضاء العينة:
S = {(H1, H2), (H1, T2), (T1, H2), (T1, T2)}.
ويمكنك تحديد النتائج بدقة بأنه لو كان لديك عدد n من العملات، فإن عدد النتائج المحتملة 2 أس n.
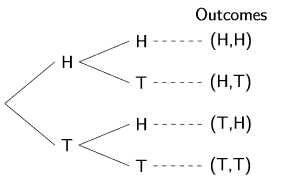
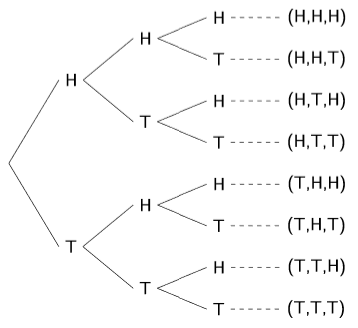
فإذا رميت عملة معدنية ثلاث مرات متتالية، فإن (n = 3). فسيكون عدد النتائج المحتملة (8 = 3^2).
مثال آخر: عند رمي قطعة نرد واحد، فهي لها 6 أوجه أي 6 نتائج، لذا ففضاء العينة سيكون: S = {1, 2, 3, 4, 5, 6}
ما هي «الأحداث-Events» في التجربة؟
في دراسة الاحتمال، لا نهتم فقط بالنتائج التي في فضاء العينة ككل بل أيضًا بمجموعات مختلفة من النتائج من فضاء العينة.
«الحدث-Event»: هو أي مجموعة (مجموعة فرعية) من النتائج -لتجربة معينة- الموجودة في فضاء العينة، يكون الحدث بسيطًا إذا كان يتكون من نتيجة واحدة بالضبط ومركبًا إذا كان يتكون من أكثر من نتيجة. ويقع احتمال وقوع أي حدث بين 0 و1.
مثال: عند رمي عملة ثلاث مرات متتاليات، فإن فضاء العينة سيكون:
S = {(T, T, T), (T, T, H), (T, H, T), (T, H, H ), (H, T, T ), (H, T, H), (H, H, T), (H, H, H)}.
فإذا أردنا إيجاد النتائج التي تحوي رأسان فقط (H) على الأقل، فستكون هكذا:
E = { (H, T, H) , (H, H, T) , (H, H, H) , (T, H, H)}.
وهذا هو الحدث، مجموعة فرعية من فضاء العينة يُرمز له بـ (E).
ما هو احتمال وقوع الحدث؟
ذكرنا سابقًا أن احتمال وقوع أي حدث يكون بين 0 و1، فـ 1 إذا كان احتمال وقوع الحدث مؤكدًا بنسبة 100٪ و0 إذا كان العكس (التجارب العشوائية مثل رمي قطعة نرد لا تخضع لأي من الرقمين لكن نتيجة وقوع أي حدث تكون بينهما). لذا فببساطة، نحصل على احتمال حدث معين A من تجربة من عدد الطرق التي يمكن أن يحدث بها A مقسومًا على العدد الإجمالي للنتائج المحتملة. ففي المثال السابق يكون احتمال وقوع حدث أن تكون هناك رأسان على الأقل هو: 8÷4= 2÷1.
أنواع الأحداث في الاحتمال
ذكرنا في البداية أن هناك نوعين أساسيان وهما المركب والبسيط وسنتعرف عليهم بالتفصيل وعلى أنواع أخرى من الأحداث الاحتمالية المهمة.
«أحداث مؤكدة ومستحيلة-Impossible and Sure Events»
إذا كان احتمال حدوث حدث هو 0، فإن هذا الحدث يُسمى حدثًا مستحيلًا وإذا كان احتمال حدوث حدث هو 1، فإنه يُسمى حدثًا مؤكدًا. بمعنى آخر، المجموعة الفارغة ϕ هي حدث مستحيل وفضاء العينة S هي حدث أكيد.
«أحداث بسيطة-Simple Events»
يُعرف أي حدث يتكون من نقطة واحدة (outcome or sample point or element or member) من فضاء العينة بأنه حدث بسيط في الاحتمال. فمثلًا:
إذا كان S = {5, 6, 7, 8, 9} و E = {7}، فإن E هو حدث بسيط.
«أحداث مركبة-Compound Events»
على النقيض من الحدث البسيط، إذا كان أي حدث يتكون من أكثر من نقطة واحدة من فضاء العينة، فإن هذا الحدث يسمى حدثًا مركبًا. فمثلًا:
S = {5, 6, 7, 8, 9}, E1 = {5, 6}, E2 = {7, 8, 9}.
إذن E1 وE2 يمثلان حدثان مركبان.
«الأحداث المستقلة والتابعة-Independent and Dependent Events»
إذا كان وقوع أي حدث لا يتأثر بحدوث أي حدث آخر، تُعرف هذه الأحداث على أنها «أحداث مستقلة» وتعرف الأحداث التي تتأثر بأحداث أخرى بـ «الأحداث التابعة».
«أحداث متنافية-Mutually Exclusive Events»
إذا كان وقوع حدث واحد يستبعد حدوث حدث آخر، فإن مثل هذه الأحداث تكون «أحداثًا متنافية-Mutually exclusive events» (أي لا يوجد أي نقطة مشتركة بين حدثين). فمثلًا، إذا كانت
S = {1, 2, 3, 4, 5, 6}.
وE1 وE2 حدثين، حيث:
E1 = {1, 2, 3} – E2 = {4, 5, 6}.
فهنا لا يوجد أي نقاط مشتركة، فـ E1 وE2 حدثان متنافيان.
«أحداث شاملة-Exhaustive Events»
الأحداث الشاملة هي مجموعة من الأحداث في فضاء العينة بحيث يحدث أحدها على نحو إلزامي أثناء إجراء التجربة. أي أن جميع الأحداث المحتملة في فضاء عينة من التجربة تشكل أحداثًا شاملة. فمثلًا، أثناء إلقاء عملة معدنية، هناك نتيجتان محتملتان. لذلك، فإن هاتين النتيجتان، هما حدثان شاملان لأن أحدهما سيحدث بالتأكيد أثناء قلب العملة. وليس من الضروري أن يكون للأحداث احتمالية متساوية لتكون شاملة، فعند رمي حجر نرد هناك 6 نتائج وهم {1, 2, 3, 4, 5, 6} وسيكون أي من هذه الأرقام هو النتيجة بالتأكيد، فإن كل هذه النتائج الست هي أحداث شاملة. لذلك، فأن اتحاد الأحداث الشاملة يعطي فضاء العينة بأكملها.
«الأحداث التكميلية-Complementary Events»
لأي حدث E1، يوجد حدث آخر ‘E1 والذي يمثل العناصر المتبقية من فضاء العينة S.
E1 = S – E1′.
مثال: إذا رمينا حجر نرد، فسيكون فضاء العينة:
S = {1, 2, 3, 4, 5, 6}
إذا كان الحدث E1 يمثل جميع النتائج التي تكون أكبر من 4، فإن E1 = {5, 6} و E1‘= {1, 2, 3, 4}.
وبالتالي فإن ‘E1 هو مكمل للحدث E1، وبالمثل مكملة E1, E2, E3… En هي’E1′, E2’, E3’… En.
الأحداث المرتبطة بـ “أو-OR”
إذا ارتبط حدثان E1 و E2 بـ «أو-OR»، فهذا يعني أنه إما E1 أو E2 أو كلاهما. يستخدم رمز الاتحاد (∪) لتمثيل «أو-OR» في الاحتمال. بالتالي، يشير الحدث E1 U E2 إلى E1 أو E2.
الأحداث المرتبطة بـ “و-And”
إذا ارتبط حدثان E1 و E2 بـ «و-AND»، فهذا يعني تقاطع العناصر المشتركة لكلا الحدثين. يستخدم رمز التقاطع (∩) لتمثيل «و-AND» في الاحتمال.بالتالي، فإن الحدث E1 ∩ E2 يشير إلى E1 و E2.
الحدث E1 – E2
يمثل رمز (-) الفرق بين كلا الحدثين. فحينما نقول E1 – E2 نقصد جميع النتائج الموجودة في E1 والتي ليست موجودة في E2. فمثلًا:
E1 = {2, 4, 6}, E2 ={2, 3, 6}. E1 – E2 ={4}.
ما هي أنواع الاحتمال؟
هناك أنواع مختلفة من الاحتمالات بناءً على طبيعة النتيجة أو النهج المتبع أثناء العثور على احتمال وقوع حدث ما. يمكن دراسة نظرية الاحتمالات بعدة طرق وسنبدأ بثلاث طرق أساسية وهما:
الاحتمال النظري (الكلاسيكي)
الاحتمال النظري هو المرتبط بالنظرية الكامنة وراء الاحتمال. للعثور على احتمال وقوع حدث باستخدام الاحتمال النظري، لا يلزم إجراء تجربة. فهو يعتمد على الرياضيات البحتة. فمثلًا إذا كان لدينا صندوق يحوي 10 كرات حمراء وزرقاء، فإن بالاحتمال النظري احتمال سحب كرة حمراء هو 10/20 = 1/2. (عدد الكرات الحمراء على المجموع الكلي للكرات).
الاحتمال التجريبي
الاحتمال التجريبي هو احتمال يتم تحديده على أساس سلسلة من التجارب. نُجري تجربة عشوائية ونُكررها عدة مرات لتحديد احتمالية حدوثها ويعرف كل تكرار على أنه تجربة. ففي المثال السابق بعد تجربة السحب السادسة وجدنا أن 4 من الكرات المسحوبة حمراء واثنين من الكرات زرقاء، هنا اختلفت النتائج عن الاحتمال النظري.
الاحتمال البديهي
الاحتمال البديهي هو نظرية احتمالية موحدة، يحدد مجموعة من البديهيات (القواعد) التي تنطبق على جميع أنواع الاحتمالات، بما في ذلك الاحتمال التجريبي والاحتمال النظري. البديهيات الثلاثة هي:
- البديهية الأولى: توضح أن بالنسبة لأي حدث A، يكون احتمال A أكبر من أو يساوي الصفر، لأنه كما ذكرنا أن أي حدث يقع بين 0 و1 و0 حدث مستحيل الوقوع و1 مؤكد الوقوع.
- البديهية الثانية: توضح أن جميع النتائج المحتملة في فضاء العينة تساوي 1.
- البديهية الثالثة: توضح أنه إذا كان A1 و A2 نتيجتان متنافيتان، فإن:
P (A1 ∪ A2) = P (A1) + P (A2).
لذا فاحتمال حدوث A1, A2, A3… يساوي مجموعهم.

وهكذا انتهينا من المقدمة في قوانين الاحتمالات، دعونا نختم بهذا المثال المجمع والذي ستتضح فيه تفاصيل أخرى، حيث هناك أنوا أخرى، فقد تكون الاحتمالات إما هامشية أو مشتركة أو مشروطة، وفهم الاختلافات بينهم هو مفتاح لفهم أسس الإحصاء (انظر للصورة أدناه).
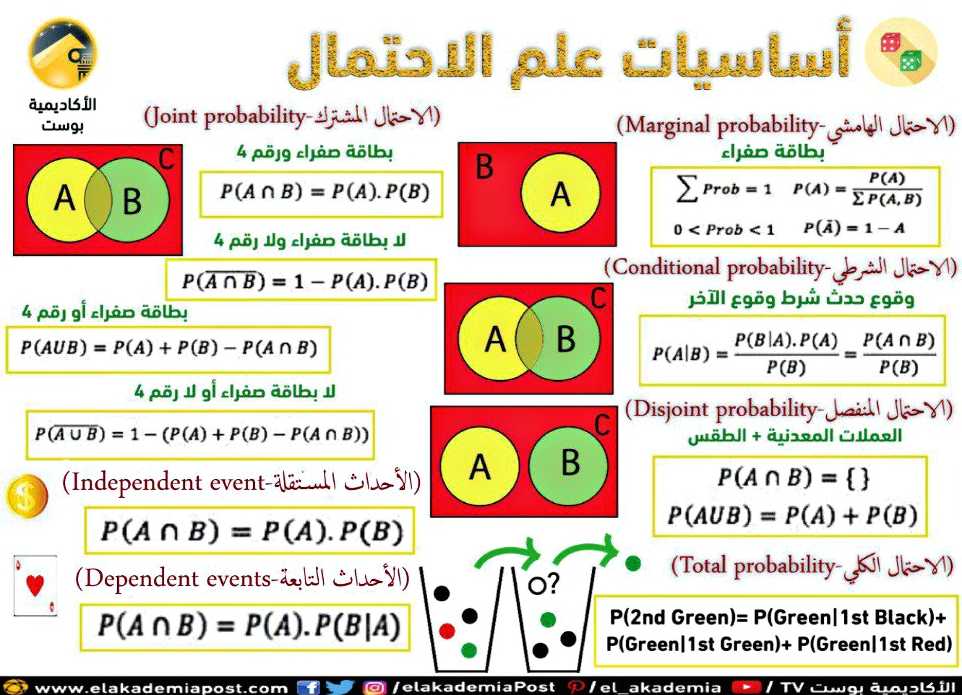
«الاحتمال الهامشي-Marginal probability»
احتمال وقوع حدث P(A)، يُنظر إليه على أنه احتمال غير مشروط. لا يشترط على حدث آخر.
مثال: احتمال أن تكون البطاقة المسحوبة صفراء من 52 بطاقة صفراء وحمراء (26 منها حمراء و26 منها صفراء) هو 1/2. والقوانين في الأعلى -بالصورة- في الاحتمال الهامشي هي الأساسية كما وضحنا سابقًا.
«الاحتمال الشرطي-Conditional probability»
يُعرَّف الاحتمال الشرطي بأنه احتمال وقوع حدث أو نتيجة، بناءً على حدوث حدث أو نتيجة سابقة، والصيغة العامة:
P(A|B) = P(A∩B)/P(B).
أو
P(B|A) = P(A∩B)/P(A).
مثال:
S ={1, 2, 3, 4, 5, 6}, A ={2,4, 6}, B ={2, 3}.
P(A|B) = P(A∩B)/P(B) = (1/6)÷(2/6) = 1/2.
(احتمال أن A يحدث بشرط أن يحدث B، أولًا التقاطع يساوي عدد عناصر الحدث على فضاء العينة، وP(B) يساوي عدد العناصر على فضاء العينة).
«نظرية بايز-Bayes Theorem»
هي نظرية في الاحتمالات والإحصاءات، سميت على اسم عالم الرياضيات البريطاني «توماس بايز-Thomas Bayes»، في القرن الثامن عشر والتي تساعد في تحديد احتمال وقوع حدث يعتمد على بعض الأحداث التي حدثت بالفعل. نظرية بايز لها العديد من التطبيقات مثلًا في قطاع الرعاية الصحية؛ لتحديد فرص تطوير المشاكل الصحية مع زيادة العمر.
تنص نظرية بايز على أن الاحتمال الشرطي لحدث A، نظرًا لحدوث حدث B آخر، يساوي ناتج احتمالية B، مع الأخذ في الاعتبار A واحتمال A.
الفرق بين صيغة الاحتمال الشرطي ونظرية بايز
الاحتمال الشرطي هو احتمال وقوع حدث “A” يعتمد على وقوع حدث آخر “B”. الصيغة:
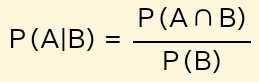
نظرية بايز: اشتقت نظرية بايز باستخدام تعريف الاحتمال الشرطي، تشتمل صيغة النظرية على احتمالين شرطيين. الصيغة:
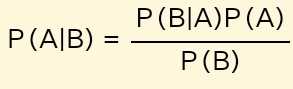
«الاحتمال المشترك-Joint probability»
هو احتمال وقوع الحدث A والحدث B. أي احتمال تقاطع حدثين أو أكثر.
مثال: احتمال أن تكون البطاقة المسحوبة صفراء (من 52 بطاقة و26 منهم حمراء و26 صفراء) وعليها الرقم 4 هو P (four and red) = 2/52 = 1/26، نفرض هنا أن B هو احتمال أن البطاقة صفراء وA هو احتمال ظهور الرقم 4.
P(A∩B) = P(A).P(B) = (4/52).(26/52) = 1/26.
السابق قانون التقاطع عندما نقول (بطاقة صفراء ورقم 4)، ماذا لو قلنا (بطاقة صفراء أو رقم 4)؛ حينها سنطبق قانون الاتحاد وقانون:
P(AUB) = P(A) + P(B) – P(A∩B).
من ثم عند الإتيان بالمكملة، نطرح كل ما سبق من 1، فإذا قلنا لا بطاقة حمراء ولا رقم 4؛ سيكون القانون التالي:
P(A’∩B’) = 1 – P(A).P(B).
وإذا قلنا لا بطاقة حمراء أو رقم 4، سيكون القانون التالي:
P(A’UB’) = 1 – P(A) + P(B) – P(A∩B).
«الاحتمال المنفصل-Disjoint probability»
وذلك يكون حينما يكون الحدثان متنافيين أو منفصلين ولا يحدث كلاهما في نفس الوقت، ومن أشهر الأمثلة هي عند رمي عملة واحدة مرة واحدة، فلن يظهر سوى وجه واحد ويستحيل ظهور الرأس والذيل معًا.
ولو فرضنا أن A تعبر عن عملات معدنية وB هو الطقس -حدثان متنافيان ولا علاقة لهم ببعضهما- ولاحظ القوانين التالية:
عند تقاطعهم سيعطينا المجموعة الخالية أو ϕ.
P(A∩B) = ϕ أو { }.
عند الاتحاد سيعطينا مجموعهما:
P(AUB) = P(A) + P(B).
«الأحداث المستقلة-Independent events»
سبق وذكرنا أن الأحداث المستقلة التي لا تعتمد على ما حدث من قبل، أي لا تتأثر هذه الأحداث بالنتائج التي حدثت سابقًا.
«الأحداث التابعة-Dependent events»
الأحداث التابعة هي التي تعتمد على ما حدث من قبل، أي تتأثر هذه الأحداث بالنتائج التي حدثت سابقًا، وإذا تغير حدث ما بالصدفة، فمن المحتمل أن يختلف الآخر. وتعبر (B|A)P أن احتمال حدوث B في حالة حدوث A أي يعتمد عليه. لاحظ القوانين بالصورة…
نهايةً، لو أردت «الاحتمال الكلي-Total probability» فهو يساوي مجموع كل الاحتمالات الموجودة.
المصادر
- Jay L. Devore, Probability and statistics, Eighth Edition, Page (50:73).
- investopedia
- bujus
- cuemath
- investopedia
- nicholas.duke
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.

التعليقات :