ما هي اللانهاية؟ وكيف أسهم جورج كانتور وجاليليو في اللانهايات؟

ما هي اللانهاية؟ وكيف أسهم جورج كانتور وجاليليو في اللانهايات؟

يكشف تاريخ اللانهاية الستار عن العقل الفضولي للإنسان. كيف فكرنا في هذه الفكرة لآلاف السنين ولسنا قريبين من الإجابة الآن كما كنا منذ آلاف السنين؟ ومع ذلك، ما زلنا مفتونين بفكرة ورمزية اللانهاية.

 لطالما عُومل مفهوم اللانهاية بمزيجٍ من الرهبة والإبهار بل ساوى البعض بينه وبين الألوهية ويرى آخرون أنه مفهوم ليس له قيمة عملية في العالم الحقيقي، بحجة أنه حتى الرياضيات التي تعتمد على ما يبدو على اللانهاية مثل حساب التفاضل والتكامل يمكن جعلها تعمل باللجوء إلى كميات لا تنضب ولكنها محدودة. لم يبد الإغريق القدماء ارتياحًا لهذا المفهوم بل أطلقوا عليه اسم «أبيرون-Apeiron»، الذي يحمل نفس النوع من الدلالات السلبية التي نطبقها الآن على كلمة الفوضى. كان “الأبيرون” مفهومًا خارج نطاق السيطرة، وحشي وخطير.

يحمل رمز اللانهاية معنى عميقًا للروحانية والحب والجمال والقوة، ففي بلاد الهند القديمة والتبت، مثّلت اللانهايةُ الازدواجيةَ والوحدة بين الذكر والأنثى. عندما يتعلق الأمر بالعلاقات الحميمية، لا يتوانى الشعراء والأدباء في وصف شعورهم نحو محبوباتهم بأنه أبديٌ سرمديٌ، بل نحن الأناس العاديون والذي لا يمتلك معظمنا ذائقة أدبية، نود أن نصدق أن الحب بين الرجل والمرأة لا حدود له.  أدى هذا القياس الجميل إلى ظهور هدايا مثل الأساور والأقراط والساعات وغيرها من المجوهرات التي تحمل رمز اللانهاية وغالبًا ما يرتدي الأزواج هذه القطع كتمثيل مادي لروحين مرتبطين بالحب الأبدي. في هذا المقال سنمضي معًا في جولة تاريخية لنعرف المعنى العميق لمفهوم اللانهاية في الرياضيات وكيف تطور هذا المفهوم عبر القرون الماضية وسنتعرف عن إسهامات أرسطو وجاليليو وكانتور في مجال اللانهايات.

سوار زينة على شكل رمز اللانهاية منقوش عليه عبارة ” لربما نلتقي مجددًا”، العبارة المشهورة من مسلسل The 100

ما هي اللا نهاية؟

تعرف اللا نهاية ببساطة بأنها الشيء اللا محدود وغير قابل للعد. نحمل جميعنا فكرة عن ماهية اللا نهاية، فهي صفة للأشياء غير المنتهية، كون لا نهائي، أو قائمة لا نهائية، كمجموعة الأعداد الطبيعية 1، 2، 3، 4، … فمهما استمريت بالعدّ، فلن تصل للنهاية أبدًا، كما أنه من المستحيل أن تصل إلى نهاية الكون حتى لو سافرت بواسطة أسرع مركبة

فضائية، وهذا النوع من اللا نهايات هو ما سمّاه العالم الرياضي الإغريقي «أرسطو-Aristotle» باللانهاية الممكنة: هذه النهاية موجودة فعلًا، لكن من المستحيل أن تصل إليها.   صنّف أرسطو نوعاً آخر من اللانهايات يُسمى باللانهاية الفعلية والتي تصف الأشياء التي باستطاعتنا قياسها، مثلًا قياس درجة حرارة جسم ما في مكان ووقت معين. لم يسبق لأحد الوصول إلى لانهاية فعلية مطلقًا، ويعتقد أرسطو أن اللانهاية الفعلية غير موجودة في العالم المادي، وحتى هذا اليوم لا يعلم الفيزيائيون مدى صحة اعتقاده.

مفهوم أرسطو للا نهاية

لقد تطلب الأمر من أرسطو أن يضع مفهوم اللانهاية بشكل دقيق بحيث لا يكاد أحد يعطيه اعتبارًا مباشرًا مرة أخرى حتى القرن التاسع عشر. كان النهج الذي اتخذه عمليًا بشكل مدهش. قرّر أرسطو أن تكون اللانهاية موجودة، لأنه بدا أن الزمن ليس له بداية ولا نهاية، كما لم يكن من الممكن القول أن أرقام العد لها نهاية على الإطلاق. إذا كان هناك رقم أكبر -أطلق عليه “max”، فما الخطأ في max + 1 أو max + 2؟ ولكن من ناحية أخرى، لا يمكن أن توجد اللانهاية في العالم الحقيقي. وقال إنه إذا كان هناك -على سبيل المثال-جسد مادي غير محدود، فسيكون بلا حدود ومع ذلك، يجب أن يكون للكائن حدودًا.

كان الحل الوسط الذي طوره أرسطو -وهو حل ذكي -هو القول إن اللانهاية موجودة وغير موجودة. وقال إنه بدلاً من أن تكون ملكية حقيقية لأي شيء حقيقي، كان هناك احتمال لانهائي. يمكن أن يكون اللانهاية من حيث المبدأ، ولكن من الناحية العملية لم يكن كذلك. يعطينا أرسطو مثالاً ممتازًا لتوضيح ذلك. الألعاب الأولمبية موجودة -من المستحيل إنكار ذلك. ومع ذلك، فقد كان كائنًا أجنبيًا يظهر (أرسطو لم يتضمن في الواقع كائنًا فضائيًا في مثاله) ويسألنا “أرني هذه الألعاب الأولمبية التي تتحدث عنها”، لم نتمكن من فعل ذلك. في الوقت الحالي هم غير موجودون في الواقع لكنهم موجودون كإمكانات. وجادل أرسطو بأن اللانهاية كانت في نفس الحالة المحتملة تمامًا.

كان هذا الشكل من اللانهاية هو الذي من شأنه أن يفرز حساب التفاضل والتكامل وسيتم تضمينه عمليًا في جميع الاعتبارات الرياضية لللامحدود حتى قام العالم جورج كانتور باكتشافات ثورية في هذا الصدد والتي قادته في نهاية الأمر إلى الجنون. لكن رجلاً واحدًا خالف هذا الاتجاه مبكرًا، وهو العالم جاليليو جاليلي المشهور في مجال علم الفلك.

مفهوم غاليليو غاليلي للانهايات

بعد بدء الإقامة الجبرية في منزل جاليليو في عام 1634، إبان محاكمته بشأن عمله الهرطقي حول حركة الأرض حول الشمس، لم يتوقف جاليليو عن الكتابة. في ذلك الوقت ، أنتج الكتاب الذي يمكن القول إنه أعظم أعماله العلمية ، والذي يعادل كتاب المبادئ الرياضية لنيوتن. ، أطللق جاليليو على كتابه اسم «Discorsi e dimostrationi matematiche» ، والذي احتوى على مفاهيم جديدة أو نقاشات وتوضيحات رياضية تتعلق بعلوم جديدة. واجه جاليليو صعوبة كبيرة في نشر هذا -أوضحت محاكم التفتيش أنه لن يتم نشر أي عمل من قبل هذا المهرطق في أي بلد تحت نفوذها-. عندما تناول الناشر الهولندي العظيم «إلسفير- Elsevier» الكتاب في نهاية المطاف، أعرب جاليليو عن دهشته الكبيرة من أنه نُشر على الإطلاق، وهو ما زعم أنه لم يكن نيته أبدًا.

اتخذ الكتاب شكل محادثة بين عدد من الشخصيات إلى حد كبير حول مسائل خطيرة. لكن بعد التساؤل عما يجعل المادة متماسكة (اعتقد جاليليو أنها جيوب صغيرة من الفراغ بين جسيمات المادة)، فإنهم يتحولون، فقط من أجل المتعة، إلى طبيعة اللانهاية. يبرز جاليليو عددًا من النقاط، ومن بين هذه النقاط واحدة جديرة بالملاحظة بشكل خاص تتضمن دوران زوج من العجلات.

بدأ جاليليو بصنع عجلات ذات جوانب قليلة على سبيل المثال، يمكن أن تكون سداسية. هذه أشكال ثلاثية الأبعاد -تخيل أن الأشكال السداسية مقطوعة من صفائح من الرخام. يُثبت الشكل السداسي الأصغر على الأكبر، ويستند كل واحد منهم على سكة أفقية خاصة به.

الآن نقوم بتدوير العجلة المدمجة بحيث تتحرك إلى جانبها التالي. عندما تقوم العجلة الكبيرة بتدويرها تدور على الزاوية وتتحرك على طول المسار بطول جانب واحد. لكن ماذا حدث للعجلة الأصغر؟ لم تتحرك العجلة الكبيرة بهذه المسافة فحسب، بل تحركت العجلة الصغيرة أيضًا. يجب أن: يتم إصلاحهما معًا. ومع ذلك، عند الدوران بمقدار 1/6 من الدوران، يجب أن يتدحرج الصغير فقط على طول المسار بطول جانبه -مسافة أصغر بكثير، مميزة باللون الأحمر في الرسم التخطيطي. لتحقيق الحركة الإضافية، رُفعت العجلة الأصغر تمامًا عن المسار.

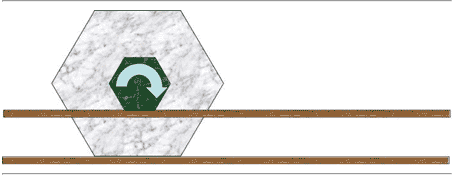
الآن هذا هو الشيء الذكي. تخيل جاليليو زيادة عدد الجوانب. كلما زاد عدد الجوانب، زادت مجموعات الحركات الصغيرة على طول القضيب والقفزات الصغيرة التي تحصل عليها أثناء تدوير العجلات. أخيرًا، دعنا نتخيل، إذا كان من الممكن، أن نأخذ هذا العدد من الأضلاع إلى ما لا نهاية. ننتهي بعجلات دائرية.

مرة أخرى نقوم بتدوير العجلتين، معًا، على طول القضبان الخاصة بهما. مرة أخرى كلاهما يقطعان نفس المسافة -في هذه الحالة ربع محيط العجلة الكبيرة-. لكن الآن حدث شيء غريب عندما دُحرجت حافة العجلة الكبيرة بمقدار ربع محيطها على مسارها، قامت حافة العجلة الأصغر بتدوير محيطها الربع الأصغر فقط، ولكن لا يزال يتعين على العجلة الصغيرة أن تقطع نفس المسافة التي تقطعها العجلة الأكبر، دون أن تترك المسار على الإطلاق. لم تكن هناك قفزات، أو على الأقل هكذا يبدو.

ما تخيله جاليليو هو أنه مع دوران العجلة الأصغر يكون هناك عدد لا حصر له من الفجوات الصغيرة متناهية الصغر، والتي تتراكم لتحدث فرقًا بين محيط العجلة والمسافة التي تتحرك فيها.  ومن هنا دخل مفهوم اللانهاية حيز اللعب في جهاز مادي لجعل ما يبدو مستحيلًا يحدث.

بعد أن ترك جاليليو هذا الأمر يتسلل إلى لاوعيه، فإن شخصية جاليليو التقليدية والقاتمة إلى حد ما، سيمبليسيو، لديها شكوى. يبدو أن ما يقوله جاليليو (أو سالفياتي تقنيًا، الشخصية التي تمثل صوت جاليليو في الكتاب) هو أن هناك عددًا لا حصر له من النقاط في عجلة دائرية واحدة وعدد لا حصر له من النقاط في الأخرى. ولكن بطريقة ما، على الرغم من أن كل منها له نفس اللانهاية من النقاط، إلا أن إحداها تضاف إلى مسافة أكبر من الأخرى. كان أحد اللانهاية هو نفسه الآخر وأكبر.

مفهوم العالم جورج كانتور للانهاية

إن جوهر حساب التفاضل والتكامل هو أنك تتعامل مع أشياء كبيرة بشكل لا نهائي. لكننا لم نضطر أبدًا إلى تحديد اللانهاية نفسها، ولم يكن علينا أبدًا القلق بشأن طبيعة اللانهاية، وذلك لأننا دائمًا ما تتعامل مع نفس النوع من اللانهاية -بالمعنى التقريبي، اللانهاية من النقاط التي تشكل خطًا، اللانهاية للجميع الأرقام الحقيقية بين 0 و1 وكان هذا محور الاهتمام في حساب التفاضل والتكامل من القرن السابع عشر إلى القرن التاسع عشر. لكن علماء الرياضيات لم يفكروا في ماهية اللانهاية، لأنهم لم يفكروا في ماهية المجموعة لسبب واحد. ما هي المجموعة؟ ثم ما هو الفرق بين مجموعة محدودة ومجموعة لانهائية؟ هذا شيء فعله العالم كانتور في أواخر القرن التاسع عشر. طور كانتور فكرة المجموعة، ومفهوم المجموعة اللانهائية، وهي المجموعة التي تحتوي على عدد لا نهائي من الأشياء.

كان الألماني جورج كانتور رائداً في الرياضيات وتحديدًا في في مجال أصبح يُعرف باسم نظرية المجموعات. وفقًا لنظرية المجموعات، فإن الأعداد الصحيحة، وهي أرقام بدون كسر أو فواصل عشرية (مثل 1، 5، -4)، تشكل مجموعة لا نهائية قابلة للعد. من ناحية أخرى، فإن الأعداد الحقيقية، والتي تشمل الأعداد الصحيحة والكسور وما يسمى بالأرقام غير النسبية، مثل الجذر التربيعي للعدد 2، هي جزء من مجموعة لا نهائية غير قابلة للعد. دفع هذا كانتور للتساؤل عن الأنواع المختلفة من اللانهاية. اعتقد كانتور أنه لا توجد نهايات بين مجموعات الأعداد الصحيحة والأعداد الحقيقية، لكنه لم يكن قادرًا على إثبات ذلك. ومع ذلك، أصبح بيانه معروفًا باسم فرضية الاستمرارية، وصُنّف علماء الرياضيات الذين عالجوا المشكلة على خطى كانتور بمنظري المجموعات

اللانهايات المعدودة والغير معدودة

ذكرنا مسبقًا أن اللانهائيات الممكنة تصف الأشياء غير المحدودة، ومن أمثلتها مجموعة الأعداد الطبيعية لكن الآن تخيل خط مستقيم طويل غير محدود. يبدأ هذا الخط من النقطة التي تقع أمامك مباشرة ويمتد إلى المالانهاية، هل اللانهاية التي يمثلها هذا الخط هي نفسها اللانهاية التي تمثلها مجموعة الأعداد الطبيعية؟

صنّف علماء الرياضيات اللانهاية الممكنة إلى لانهايات معدودة ولانهايات غير معدودة. تُمثل الأعداد الطبيعية لانهاية معدودة، وهذا منطقي لأنه باستطاعتك مواصلة العد إذا كان لديك وقت لانهائي، كما هو الحال بالنسبة لمجموعة لا نهائية من الأشخاص، بإمكانك إدراجهم في قائمة تحمل جميع اسماءهم، وكل اسم يشغل خانته الخاصة ومن ثم عدهم إذا كان لديك وقت لا نهائي أيضًا. بصورةٍ عامة يمكننا القول أنّ أيّ مجموعة غير محدودة من العناصر تمثل لانهاية معدودة إذا كان باستطاعتك إدراج تلك العناصر في قائمة، وكل عنصر لديه مكان خاص في هذه القائمة وكل مكان في القائمة يتسع لعنصر واحد فقط.  

تخيل الآن أن لدينا خط مستقيم لانهائي، أي أنه يتكون من عدد من العناصر اللانهائية أيضًا، وفي هذه الحالة تُسمى تلك العناصر نقاطاً على الخط، إذا وضعنا على الخط مسطرة طويلة لانهائية، فإن كل نقطة على الخط يمثلها عدد على المسطرة، النقطة الأولى على الخط تقع على العدد 0، النقطة التي تبعد نصف متر عن البداية تقع على العدد 0.5، وهكذا. يطلق على المجموعة العددية التي تمثلها المسطرة اسم مجموعة الأعداد الحقيقية الموجبة وهي تشمل الاعداد الطبيعية والكسور والأرقام النسبية. هل يمكنك وضع قائمة لهذه الأعداد لكي ترى إذا كانت تمثل لانهاية معدودة أيضًا؟ ربما بإمكانك ترتيب هذه الأعداد عن طريق الحجم، لكن ستزيد هذه الطريقة من صعوبة المسألة. وبالتأكيد العدد الأول سيكون 0، لكن ماذا يجب أن يكون العدد الذي يليه؟ ربما 0.1؟ لكن 0.01 أصغر منه ويجب أن يأتي قبل 0.1. لكن ماذا عن 0.001؟ لكل عدد تظن أنه من الممكن أن يحل المرتبة الثانية في القائمة سوف تجد عدد أصغر منه (ببساطة تضيف صفرًا بعد الفاصلة)، فلذلك ترتيب هذه الأعداد على المسطرة بواسطة الحجم غير مجدي.   هل من الممكن إيجاد طريقة أخرى لإدراج الأعداد في قائمة؟ الإجابة هي لا يمكن ذلك، وهناك سبب منطقي ومباشر لهذه المسألة وينص على أنه في أي قائمة لأعداد حقيقية موجبة هناك على الأقل عدد واحد مفقود، وبالتالي لا يمكنك كتابة قائمة كاملة أبدًا، وهذا يثبت أن اللانهاية الممثلة عن طريق الخط المستقيم (أو الأعداد الحقيقية الموجبة) هي لانهاية غير معدودة.

المصادر

firstscience
livescience
plus.maths
gyllenwatches
britannica
pbs.org