- ما هي الخوارزميات المستوحاة من الطبيعة واستخداماتها ؟
- الساكنة البدئية في الخوارزمية التحسينية وأهميتها؟
- كيف يتم اختيار الخوارزميات التحسينية ؟
- ما هي الخوارزميات الجينية؟
- تعرف على خوارزمية النزول التدرجي الأشهر في الخوارزميات التحسينية
- ما هي خوارزميات التخمير المحاكى وكيف تعمل؟
- لم استوحت خوارزمية البحث التناغمي من الموسيقى وكيف تعمل؟
- خوارزمية التطور التفاضلي، الخوارزمية المستوحاة من نظرية التطور!
- خوارزمية الخفاش، الخوارزمية الثورية المستوحاة من البحث بالصدى
- ما هي خوارزمية مستعمرة النمل Ant Colony Algorithm وكيف تعمل؟
- خوارزميات النحل، الخوارزميات الثورية في مجال الحوسبة التحسينية
- دليلك لفهم خوارزمية أدم ADAM التحسينية الأكثر استخدامًا في التعلم العميق
النمل حشرات اجتماعية، تعيش في مستعمرات منظمة يتراوح عدد أعضائها بين المليونين إلي خمسة وعشرون مليون نملة. وعند بحثها عن المؤن، تتعاون مجموعات النمل فيما بينها بمختلف الطرق. فنجد من بينها، تركها لمركبات كميائية ذات رائحة معينة، أو فيرومونات من أجل التواصل مع بعضها البعض. واعتمادًا على هذه الفيرومونات تستطيع كل نملة تتبع كل مسار مشبع بها. وعند إيجاد النمل لمصدر طعام تقوم بوضع علامة كيميائية، أي وضع علامة عليه باستخدام فيروموناتها، إضافة لترك آثار كيميائية في المسار المؤدي إلى المصدر ذهابًا و إيابًا لمساعدة بقية المجموعة. تلك العمليات المعقدة أدت إلى استخدام خوارزمية مستعمرة النمل Ant Colony Algorithm في حل المشكلات الحوسبية المعقدة، فكيف حدث ذلك؟ وكيف تعمل تلك الخوارزمية؟
إنطلاقًا من البحث الأولي، والذي يكون عشوائيًا والمكلف في الوقت والجهد، تتغير تركيزات الفيرومونات من مسار لأخر. فتتبع النملات الباحثة المسار الأكثر تشبعًا. ويرجع هذا التشبع إلي تزايد عدد النملات اللاتي اتخدن هذا المسار. فباتخاد النمل لمسار محدد مرة تلو الأخرى يصبح، عمليًا، المسار المفضل. وذلك يرجع بالطبع لكونه يفيض بالفيرمونات المتروكة كعلامة من كل نملة سلكته. وهكذا تظهر طرق عديدة مفضلة نحو مصادر الطعام المكتشفة، والتي تكون غالبا هي أقصر طريق. وطريقة العمل هذه عبارة عن مثال من أمثلة ميكانيزمات رد الفعل الإيجابي positive feedback mechanisms.
محتويات المقال :
السلوك المنظم للنمل
تتواجد السلوكيات المنبثقة وتتولد انطلاقًا من التفاعلات المختلفة بين النمل في المستعمرة. بحيث يتصرف أفراد المستعمرة اعتمادًا على المعلومات المحلية البسيطة المتوفرة، مثل تركيز الفيرومونات، لتنفيذ أنشطتهم.
فبالرغم من عدم تواجد رقيب يصدر الأوامر والإرشادات، نجد أن السلوك المنظم موجود لا محالة، وبتلقائية. لذلك، فسلوك من هذا القبيل ليس غريبًا في الطبيعة، ونجده حاضرًا في عدد من العمليات والظواهر الطبيعية مثل تشكل الأنماط في جلود بعض الحيوانات وتعاون الحيوانات والحشرات التي تعيش في مجموعات فيما بينها، مثل النحل والطيور، وغيرهم.

أنماط البحث الاستثنائية
تظهر أنماط البحث عن الموارد عند بعض أنواع النمل، مثل نمل الجيش army ant، مجموعة من الخصائص الاستثنائية. بحيث يقوم هذا النوع من النمل، بالبحث عن الطعام عبر عدد من الطرق الاعتيادية بزاوية فريدة وهي °123. لاعلم لنا بكيفية قدرتها على اتباع هكذا نمط و الحفاظ عليه، لكن الدراسات أظهرت أن، هذا النمل الذي ينقل مستعمرته باستمرار، يقوم مباشرة بعد انتقاله لمنطقة جديدة ببناء مستعمرته المؤقتة وبدء عملية بحثه عن الموارد.

في اليوم الأول يقوم النمل بالتجوال بطريقة عشوائية لاستكشاف محيطه، فيتحرك باتجاه معين مسافة عدة مئات من الأمتار تم يتفرع لتغطية و استكشاف مساحة أكبر. وفي اليوم التالي يختار اتجاه أخر منحرفًا عن مسار اليوم السابق بزاوية مضبوطة تساوي °123، وبالتالي تغطية مساحة كبيرة أخرى. في اليوم الذي يليه، يختار مرة أخرى اتجاه مختلفا بنفس الزاوية. بهذه الطريقة يقوم أفراد المجموعة بتغطية المنطقة كاملة في غضون أسبوعين و بعدها ينتقلون لمنطقة جديدة للاستقرار بها مؤقتًا واستكشافها والاستفادة من مواردها.
الملفت للنظر في هذا الأمر أن النمل لا يختار زاوية °120 بل °123 بالضبط، ما يكنهم بحلول اليوم الثالث من ترك زاوية °10 عن اتجاه اليوم الأول. ما يعني أن النمل سيغطي كل المنطقة الدائرية في غضون أربعة عشر يوما بدون تغطية أي مساحة تم البحث فيها مسبقا. ما يجعل من هذه الظاهرة جد رائعة وفريدة في عالم الحيونات والحشرات.
مراحل البحث في خوارزمية مستعمرة النمل Ant Colony Algorithm
للتبسيط نأخد مسارين فقط بين مصدر الطعام و المستعمرة، يمكن تحليل المراحل كما التالي:
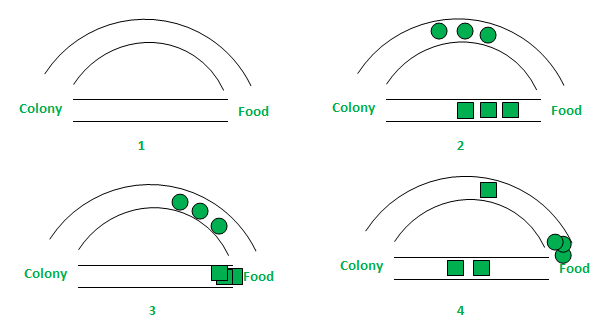
- المرحلة الأولى: كل النملات لا تزال في بيتها، ولا يوجد أي تركيز من الفيرومونات في محيطها.
- المرحلة الثانية: تبدأ النملات بحثها العشوائي أي لكل من الطريقين احتمالية مساوية للآخر في أن يؤخد، أي 0.5 في حالتنا هذه. ومن المؤكد أن الطريق الثاني أطول وبالتالي الوقت المطلوب لقطعه، والوصول للطعام، أكبر.
- المرحلة الثالثة: تصل النملات التي اتخذت الطريق الأقصر أسرع من نظيراتها، اللواتي سلكن الطريق الأطول، لمصدر الطعام. والآن من الواضح أن النمل الذي سيتبعهم في البحث سيواجه نفس المعضلة، معضلة اتخاد الطريق المناسب، لكن هذه المرة الطريق الأقصر متاح نظرًا للفيرومونات وبتركيز أعلى نظرًا لسرعة عودة النمل، وبالتالي احتمالية أعلى في اختياره.
- المرحلة الرابعة: تعود نملات أكثر وأكثر من الطريق الأقصر ما يزيد بشكل كبير من تركيز الفيرومونات في هذا الأخير. ما يقلص بشكل كبير احتمالية سلوك الطريق الأخر. وبالتالي كل المستعمرة ستستخدم الطريق الأقصر، أي أن عملية تحسين المسار قد تمت بنجاح.
آلية عمل خوارزمية مستعمرة النمل Ant Colony Algorithm
اعتمادًا على خصائص سلوكيات النمل هذه، طور العلماء عدد كبير من خوارزميات مستعمرة النمل القوية، لتحقق تقدمًا كبيرًا في السنوات الأخيرة. فانطلاقًا من السنوات التي تلت تقديمها أول مرة من طرف ماركو دوريغو Marco Dorigo، سنة 1992، كمثال ناجح للخوارزميات المستوحاة من الطبيعة، ظهر عدد ضخم من المتحورات والامتدادات لها.
فلمواجهة مشكل تجسيد هذه الخصائص بطريقة خوارزمية، نجد أنفسنا أمام مبدأين وهما احتمالية اختيار الطريق المناسب، و معدل تبخر الفيرمونات. ويوجد عدد من الطرق لفعل هذا، رغم كون هذا المشكل لا زال مطروحًا لمزيد من البحث، لكن سنتحدث عن أفضل طريقة معتمدة حاليًا.
احتمالية اختيار المسار
في مشكلة توجيه الشبكة network routing، تكون احتمالية اختيار نملة في نقطة i التوجه نحو نقطة j ممثل بواسطة الصيغة التالية:
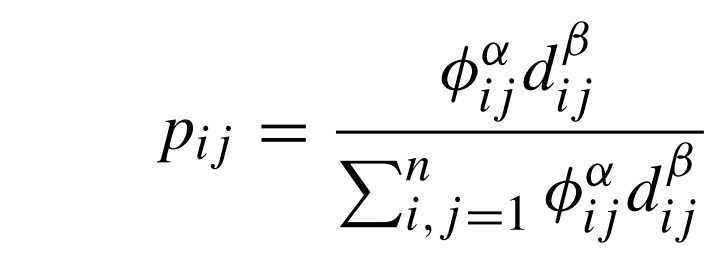
ما يعني أن المسار الأقصر هو الذي سيُسلك لكون مدة عبوره أصغر وبالتالي تركيز الفيرومونات عالٍ به. وهذه الصيغة الاحتمالية تعكس حقيقة أن النمل سيتبعون دائما المسار الأكثر تشبعًا بالفيرومونات. ففي الحالة الأبسط عند كون α=β=1، تكون هذه الاحتمالية مطابقة تماما لنسب التراكيز. وقيم المقام تقوم بمعايرة normalize هذه الاحتمالية لتحصر بين 0 و 1.
معدل تبخر الفيرومونات
يتغير تركيز الفيرومونات بمرور الزمن، فتتقلص تدريجيًا، بسبب التبخر، اعتمادًا على صيغة محددة. والأفضلية التي تكسبنا هذه الخاصية هي قدرتها على تمكيننا من تجنب الحلول المحلية. ففي أغلب حالات عدم تواجد هذه الألية، تصبح المسارات المتخذة عشوائيًا من طرف مجموعة البحث الأولى، مسارات مفضلة. وتمكننا المعادلة التالية، والتي تأخد معدل γ لاضمحلال وتبخر الفيرومونات، من تقليص هذه القيم بتقدم الزمن:
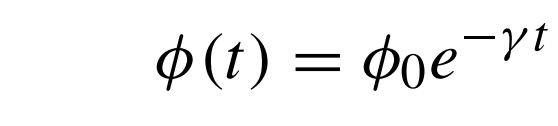
إن كانت γt أصغر بكثير من 1، و تغير الزمن Δt =1، نغير المعادلة للصيغة المبسطة التالية:
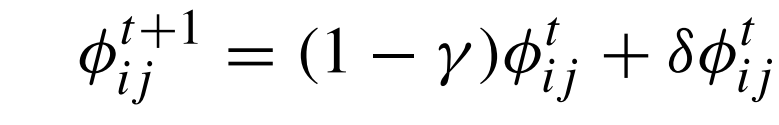
دراسة تقارب خوارزمية مستعمرة النمل
يمكن إثبات قدرة عدد من متحورات خوارزمية مستعمرة النمل Ant Colony Algorithm، على التقارب نحو الحل الأمثل للمشكل المعالج خلال مدة زمنية محدودة. لكن مثل أغلب خوارزميات الأدلة العليا Metaheuristic Algorithms، من الصعب تقدير سرعة التقارب نظريًا. وهو ما يضطرنا لدراستها تجريبيًا بتغيير معلمات ضبطها. فبهكذا دراسة تم التوصل لكون أن سرعة تنفيذ الخوارزمية جد حساسة لمعلمات الضبط هذه وخصوصًا معدل تبخر الفيرومونات.
متحورات وامتدادات
تعتبر خوارزمية مستعمرة النمل Ant Colony Algorithm من مواضيع البحث المثيرة. فنظرا لإمكانياتها الهائلة نجد أن المجتمع العلمي المتخصص قد قدم عدد ضخما من المتحورات و الامتدادات انطلاقا من الخوارزمية الأصل المطورة من طرف دوريغو، ونجد من بين أشهرها:
- الخوارزمية الأصل، خوارزمية مستعمرة النمل أو كما تمت تسميتها نضام النمل Ant System، واختصارًا AS.
- المتحور Max-min Ant System، أو اختصارا MMAS. وتختلف هذه الأخيرة عن المتحورات الأخرى، بحصر نسب الفيرمونات في كل المسارات بين مقدارين معينين، وكون الدورة الحالية الأمثل هي فقط قادرة على ترك نسب أعلى من الفيرمونات في مسارها.
- خوارزمية نظام تصنيف النمل Rank-based Ant System.
- مستعمرة النمل العمودية المستمرة Continuous orthogonal Ant System.
- خوارزميات النمل الافتراضية Virtual Ant Algorithms، لحل مشاكل التحسين التقليدية متعددة الأبعاد.
- نظام النمل النخبوي Elitist Ant System، يهدف هذا المتحور لجعل عملية الاستكشاف تتمحور حول الحل الأمثل الحالي. وذلك بجعل كل المسارات مرتبطة بالمسار الحالي الأفضل.
- خوارزمية نظام مستعمرة النمل Ant Colony System، أو ACS. بحيث تختلف عن الأصل في 3 نقط أساسية وهي: اختيار المسار منحاز لقدرتنا على استغلاله على مدار التكرارت التالية. تغير النملات معدل الفيرمونات في المسار المختار بكم مختلف من مسار لأخر. عند نهاية كل دورة، النملة الأفضل وحدها مخولة لتغيير نسب الفيرمونات في المسارات المتعددة، والتي ستتخدها المستعمرة في الدورة التالية.
تطبيقات خوارزمية مستعمرة النمل ومتحوراتها
تتكون الأنظمة المعقدة من عقد متفردة، لذلك يمكن تمديد هذه الخوارزمية لحل مشاكل توجيه جد معقدة Complex routing problems بطريق فعالة. ففي الواقع نجد أن خوارزمية مستعمرة النمل ومتحوراتها قد تم تطبيقها لحل المشكلات الضخمة الآتية:
- مشكل توجيه الإنترنت Internet routing problem.
- مشكل البائع المتجول Traveling Salesman Problem.
و أيضا عدد من المشاكل المتنوعة في مختلف المجالات نذكر منها:
- مشاكل الجدولة Scheduling Problems.
- مشاكل توجيه السيارات Vehicle Routing Problems.
- مشاكل التوزيع Assignment Problems.
- مشاكل المجموعات الرياضية Set Problems.
- تحجيم الأجهزة في تصميم إلكترونيات النانو Device sizing problem in nanoelectronics physical design.
- تصميم الأنتينات.
- معالجة الصور.
- التصميم الصناعي.
- القطاع البنكي والمصرفي.
- التنقيب عن البيانات.
و الكثير غيرها.
مصادر
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.




التعليقات :