- ما هي الخوارزميات المستوحاة من الطبيعة واستخداماتها ؟
- الساكنة البدئية في الخوارزمية التحسينية وأهميتها؟
- كيف يتم اختيار الخوارزميات التحسينية ؟
- ما هي الخوارزميات الجينية؟
- تعرف على خوارزمية النزول التدرجي الأشهر في الخوارزميات التحسينية
- ما هي خوارزميات التخمير المحاكى وكيف تعمل؟
- لم استوحت خوارزمية البحث التناغمي من الموسيقى وكيف تعمل؟
- خوارزمية التطور التفاضلي، الخوارزمية المستوحاة من نظرية التطور!
- خوارزمية الخفاش، الخوارزمية الثورية المستوحاة من البحث بالصدى
- ما هي خوارزمية مستعمرة النمل Ant Colony Algorithm وكيف تعمل؟
- خوارزميات النحل، الخوارزميات الثورية في مجال الحوسبة التحسينية
- دليلك لفهم خوارزمية أدم ADAM التحسينية الأكثر استخدامًا في التعلم العميق
تعد طريقة البحث التناغمي أحد خوارزميات الأدلة العلية الفعالة في حل المشاكل التحسينية، وذلك لكونها توفر البساطة وفاعلية البحث. فنجد أنه تم استخدامها في مواجهة عدد كبير من التحديات في مجال التحسين الحوسبي على مدار العقدين الأخيرين. اقترحها أول مرة “زونغ وو جيم ZW Geem” وزملاؤه سنة 2001، واستخدمت خوارزمية البحث التناغمي في حل الدوال التحسينية، وتصميم البنى الميكانيكية، وتحسين شبكات الأنابيب، وكذلك تحسين أنظمة تصنيف البيانات، وغيرها من التطبيقات.
وكما تشير تسميتها، فإن خوارزمية البحث التناغمي هي عبارة عن خوارزمية تحسينية استلهمت من ظاهرة طبيعية، وهي الموسيقى. فبناءً على الملاحظة استلهمت هذه الخوارزمية من فكرة أن هدف الموسيقى هو البحث عن التناغم المثالي. فكما هو معلوم، عند تأليف الموسيقيين لنغماتهم يجربون عادة عدد من التركيبات بين نغمات موسيقية معلومة من الذاكرة. هذا البحث المستمر عن النغمة المثالية انطلاقًا مما هو مكتسب عن طريق الذاكرة مماثل في الهدف والوسيلة لآلية البحث في حل المشاكل الهندسية التحسينية أي إيجاد الحل الأمثل بين عدد لا نهائي من الحلول الممكنة. ويمثل الشكل التالي ملخصًا لهذه المقاربة:

محتويات المقال :
التناغم و الترددات
تحدد هذه النغمة المثالية اعتمادًا على المعايير الجمالية للمستمع، وهو ما يستوجب ضبط جودة جمالية الأدوات الموسيقية عبر تحديد درجة النغمة pitch، أي التردد frequency، و الطابع الصوتي timbre، أي جودة الصوت quality، والذروة amplitude، أي جهارة الصوت loudness. وتحدد الدروة انطلاقًا من المحتوى التناغمي والذي يحدد بدوره بناء على الشكل الموجي وتضمين الإشارة الصوتية.
رغم ذلك سنجد أن التناغم يعتمد بالدرجة الأكبر على نطاق التردد الذي تولده الألة الموسيقية المستعملة. فباختلاف النوتات، تختلف الترددات الناتجة بالطبع. وبالتالي يتضح أن محاولة تغيير النغمة هي في الأساس محاولة لتغيير التردد الناتج، لذا ففي النظرية الموسيقية نجد أن درجة النغمة p تمثل كمقياس رقمي باستعمال الصيغة التالية:
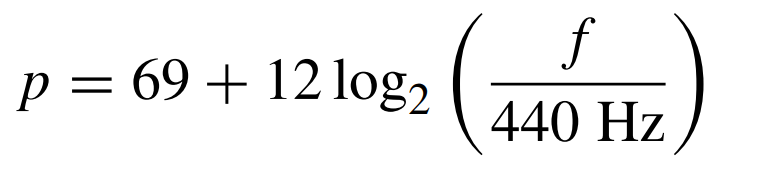
أو
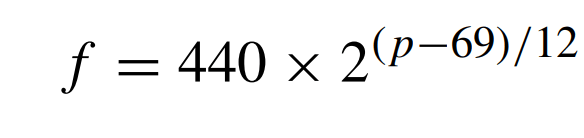
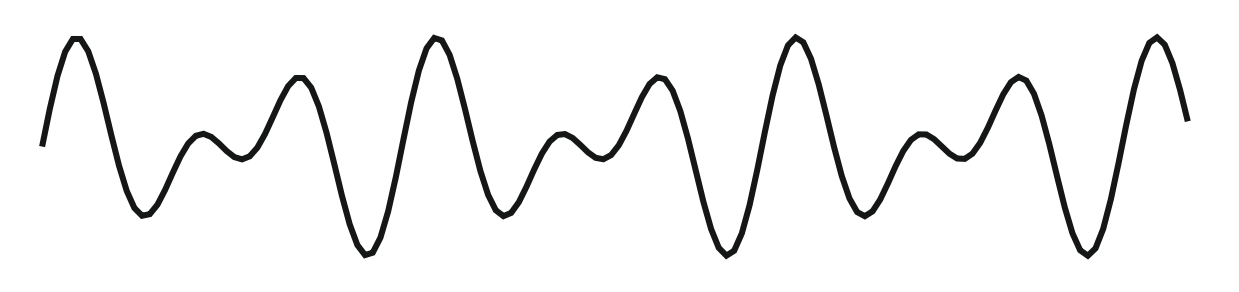

ما يعني أن ل A4 رقم نغمة يساوي 69، لأن ترددها هو 440 وبالتالي لوغاريتم 1 هو صفر ومنه p=69. وعلى هذا السلم نجد أن حجم الجواب، أو الأوكتاف هو 12 وحجم نصف النغمة هو 1. كما أن النسبة بين تردد نغمتين تبعدان جواب عن بعضهما هو 2:1. وبالتالي تردد نغمة يضاعف أو يخفض إلي النصف عند تغيرها بجواب. على سبيل المثال ل A2 تردد 110Hz، بينما تردد A5 هو 880Hz. لذا فرغم كون تحديد الجمالية أمر غير موضوعي ويعتمد على أذن السامع، يمكننا وضع تقدير معياري لتقدير التناغم. وذلك بالاعتماد على نسبة التردد المنسوبة لعالم الرياضيات اليوناني القديم فيثاغورس.
كمثال نجد أن جواب بنسبة تردد 1:2 جذاب عند لعبه معا، نفس الشيء لنسبة التردد 2:3. لكن من غير المرجح لأي نغمة عشوائية مثل الممثلة أعلاه أن تصدر أي صوت جميل.
ألية عمل خوارزمية البحث التناغمي
يمكن تفصيل خوارزمية البحث التناغمي استنادًا للظاهرة المبنية عليها، أي ارتجال الموسيقي لألحانه. فعند ارتجال هذا الأخير لنغماته، يجد نفسه أمام ثلاث اختيارات لتحقيق مراده. أولها، لعب مقطوعة موسيقية معروفة من الذاكرة، أي تأدية سلسلة من الألحان المتناغمة فيما بينها دون إضافة أو تغيير. ثانيًا، يمكنه تأدية قطعة قريبة من القطعة المعروفة، أي بتغيير طفيف في النغمات. أو ثالثًا، يمكنه تركيب عدد من الألحان المختلفة ومحاولة إيجاد تناغم فيما بينها.
بناء على هذا، إذا ما عممنا اختياراتنا الثلاث هذه من أجل التحسين، نحصل على ثلاث مكونات مكافئة وهي: الذاكرة التناغمية، وضبط النغمات، وخلق العشوائية.
1. الذاكرة التناغمية
استعمال الذاكرة التناغمية أمر جد مهم بحيث يكافئ ذلك اختيار الأفراد الأصلح بين أفراد الساكنة الحالية في الخوارزميات الجينية. ما سيضمن على مر التنفيذ أن النغمات الأمثل ستحفظ وتستمر في الذاكرة التناغمية عند الجيل الجديد، أي دورة التنفيذ التالية. ولاستعمال هذه الذاكرة بفاعلية أكبر يمكننا وضع معلمة ضبط r محصورة بين 0 و 1، ونطلق عليها معدل الاعتبار أو نسبة قبول الذاكرة التناغمية. إن كانت هذه النسبة جد صغيرة سيتم اختيار عدد قليل فقط من النغمات المثلى للاستمرار، مما سيؤدي بنا لتباطؤ معدل التقارب. لكن إن كانت هذه القيمة كبيرة جدًا، أي تقارب 1، حينها سيتم استعمال كل النغمات الناتجة وتوجيهها للذاكرة التناغمية لكن دون استكشاف جيد لنغمات محتملة أخرى، ما يؤدي لإمكانية التوصل لحلول خاطئة وغير دقيقة. لهذا نستعمل عموما كقيمة ل r قيم بين 0.7 و 0.95.
2. ضبط النغمات
لتعديل النغمة قليلًا، في المكون الثاني، نستعمل طريقة تمكننا من ضبط التردد بكفاءة. نظريا يمكن تعديل النغمة بطريقة خطية أو غير خطية. لكن في التطبيق نجد أن التعديل الخطي هو المستعمل. باعتبار X old هي النغمة الحالية، نجد أن النغمة الجديدة X new تولد بواسطة الصيغة أدناه:
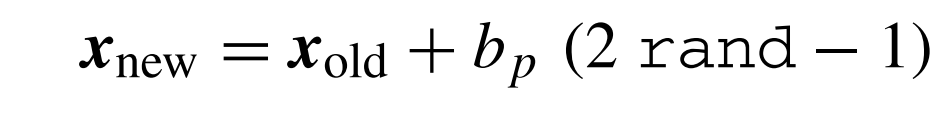
عند الملاحظة، نجد أن تعديل النغمة مماثل لعامل التطفر في الخوارزميات الجينية. وفي نفس السياق يمكننا وضع معامل لضبط معدل التعديل rpa للتحكم في درجة الضبط. وإن كان هذا المعامل جد منخفض، فلن يكون هناك تغيير ملحوظ على النغمة. لكن إن كان جد مرتفع، فقد لا تتقارب الخوارزمية، لأن التغيير سيكون جذري. لهذا، في أغلب التطبيقات، نضع هذا المعامل بين 0.1 و 0.5.
3. خلق العشوائية
أما المكون الثالث، وهو العشوائية، يهدف إلي زيادة تنوع الحلول الناتجة. فرغم أن لضبط النغمة دور مماثل إلا أن هذا الضبط محصور في ضبط محلي وبالتالي بحث محلي. إذا، يقودنا استعمال العشوائية إلى البحث في مناطق مختلفة، مما يوفر تنوعًا كبيرًا في الحلول، وبالتالي، يزيد من احتمالية إيجادنا للحل الأمثل. ويمكن تلخيص هذه المكونات الثلاث في أربع خطوات:
- استهلال الذاكرة التناغمية بعدد من الحلول العشوائية الممكنة، مثل الساكنة البدئية في الخوارزميات الجينية.
- ارتجال حلول جديدة.
- تحديث الذاكرة التناغمية الحالية، باستبدال الحلول المرتجلة الجيدة بالحلول الأسوأ.
- إعادة الخطوتين الثانية والثالثة إلي أن يتحقق شرط من شروط إنهاء التنفيذ، أي عدم إيجادنا لنغمات جيدة بعد عدد من التكرارت، أو بلوغ الحد الأقصى من التكرارات.
متحورات خوارزمية البحث التناغمي
على مر العقدين الأخيرين تم دراسة عدد كبير من متحورات خوارزمية البحث التناغمي بهدف تعزيز أدائها في مواجهة المشاكل المختلفة في مجال التحسين الحوسبي. وكأمر ضروري نجد أن “جيم”، مطور هذه الخوارزمية، قد قدم متحورًا لمعالجة المشاكل المعنية بالمتغيرات المتقطعة أي فضاءات البحث غير المستمرة وذلك بتقديم مشتقات تصادفية للمتغيرات المتقطعة. وبالطبع لا يقصد بالاشتقاق هنا الاشتقاق التقليدي في الرياضيات، بل الفرق بين نقطتين فقط. وباستعمال هذه المشتقات نحدد عدد من الاحتماليات التي تخص كل نغمة من نغمات الذاكرة الحالية، أي الذاكرة التناغمية. فنجد أن هذا المتحور قد استخدم في المشكل التحسيني الذي يخص التصميم الأمثل لقنوات نقل الموائع.
وفي نفس السياق نجد أنه قد تم تطوير عدد كبير من المتحورات من طرف عدد من المتخصصين وغير المتخصصين لحل مشاكل جد محددة، وفي أحيان أخرى تقديم إطار عام لحل مجموعة من المشاكل المتشابهة.
الخوارزميات الهجينة
يتم تطوير الخوارزميات الهجينة بدمج خوارزميتان أو أكثر بهدف تعزيز الكفاءة والأداء عموماً. فيهدف الباحثون دائما لاستغلال مميزات الخوارزميات لتحقيق الصالح المشترك أو على الأقل يبقى هذا هدفهم البدئي. لكن في الواقع لا يزال فعل هذا مشكلة بلا حل. رغم كل هذا، لا يوجد ما يمنعنا من استلهام الطرق الخوارزمية الأخرى وتحسين أداء خوارزمياتنا.
وقد قدم عمران ومادهافي المتحور Global-best Harmony Search مستلهمين أفكارًا من خوارزميات استمثال عناصر السرب Particle Swarm Optimization. في هذا المتحور يقوم تعديل النغمة انطلاقا من أفضل حل من الذاكرة التناغمية فقط، بدون اعتبار لعرض النطاق bp. وهو ما أضاف قدرات تعلم اجتماعي social learning فريدة لهذه الطريقة. وقد تم التأكد من أن أداء هذا المتحور أفضل من أداء الخوارزمية الأصل تجريبيًا.
تقدم الخوارزمية المتحورة DLHS Dynamic Local-best Harmony Search مقاربة خوارزمية تنطوي على تقسيم الساكنة الحالية إلي ساكنات فرعية، تتطور بشكل مستقل عن بعضها البعض. غير أن هذه الذاكرات الفرعية تجتمع لتكوين الذاكرة التناغمية الحالية بعد بحثها عن الحل الأمثل على حدى في مجالاتها المحلية الخاصة، مستوحاةً من النسخ المحلية لخوارزمية استمثال عناصر السرب PSO والمتحور GHS، ومقترحةً من طرف “كوان كي بان” وزملائه.
من خلال سياستها هذه واستراتيجية البحث المحلية المبسطة ، فإن المتحورة DLHS قادرة على تحقيق توازن مرضٍ بين الاستكشاف exploration والاستغلال exploitation في البحث. فنجد من بين تطبيقاتها أنها طبقت بنجاح لمواجهة مشكل الجدولة lot-streaming flow shop القائم على تقسيم عملية ما لمجموعة من العمليات المصغرة والتي تنفذ بطريقة متداخلة.
وعلى هذا المنوال، نجد العديد من المتحورات الأخرى التي استلهمت من سابقاتها منها Particle Swarm Harmony Search PSHS من طرف جيم. وإلخ.
تطبيقات خوارزمية البحث التناغمي
في العالم الحقيقي، يفيض العلم الحديث والصناعة بالمشاكل التحسينية المختلفة. فمنذ أن تم اقتراح الخوارزمية أول مرة من طرف جيم وتطبيقها لحل مشكلة تحسين شبكات توزيع المياه عام 2001، نجحت الخوارزمية في تغطية تطبيقات العديد من المجالات بما في ذلك الصناعة، ومعايير التحسين، وأنظمة الطاقة، والعلوم الطبية، وأنظمة التحكم، وتصميم البناء، وتكنولوجيا المعلومات.
مصادر
Hindawi
ScienceDirect
Nature Inspired Optimization Algorithm by Xin She Yang
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.




التعليقات :