يُعزى الفضل في النهضة الأوروبية إلى علوم منها التفاضل والتكامل. فلولاهما لما كنت تستخدم هاتفك الآن لقراءة هذا المقال مثلًا، فتطببقاتهما لا تُعد. فنحن بحاجة دائمة إليهما لفهم نماذج المناخ أو النمو السكاني أو انتشار الأمراض أو آليات حل النزاعات أو التعامل مع الأزمات الاقتصادية والمالية وغيرها من الأمور. كما ستجد تطبيقاتهما في أغلب العلوم. إذ يمثل التفاضل والتكامل العمود الفقري للتعامل مع المشكلات. وفي هذا المقال ستعرف عن كيفية بدء التفاضل والتكامل؟ وما الفرق بينهما؟ إضافةً إلى التطرق لأحد أهم المفاهيم التي أسهمت في بناء التفاضل والتكامل. والتعرف على المعادلة الخاصة به ألا وهي النهايات Limits، كأحد أشهر المعادلات الرياضية في التاريخ.
محتويات المقال :
ما هو التفاضل والتكامل؟
باختصار، يقيس التفاضل والتكامل معدل التغير الذي يحدث في كل ظاهرة بالكون تقريبًا. وينقسم إلى تكاملات ومشتقات. فالتكامل عملية عكسية للتفاضل، فالتفاضل معني بتقسيم الدالة إلى أجزاء، بينما يُستخدم التكامل لتوحيد تلك الأجزاء، لتشكيل الدالة الأصلية. أما هندسيًا، فيستخدم التفاضل والتكامل لإيجاد ميل المنحنى أو المساحة الواقعة أسفل المنحنى. ويعمل التفاضل على تحديد معدل التغيير كإيجاد ميل الدالة عند نقطة ما. بينما التكامل معني بإيجاد المنطقة الواقعة تحت منحنى دالة.
وهناك بنية تحتية تحمل هذين الفرعين وقبل معرفة أحد هذه الركائز وهي «النهايات-Limits». والآن، لنفهم جيدًا المراحل التي مر بها علم التفاضل والتكامل ومن أين خرجت لنا النهايات وما فائدتها؟
علماء التفاضل والتكامل
ربما مرت على مسامعك معلومة أن العالم البريطاني إسحاق نيوتن والعالم الألماني جوتفريد لايبنتز هما من وضعا المبادئ الأساسية للتفاضل والتكامل في القرن ال17، وطور كلا منهما هذه الأساسيات على نحو مستقل. لذلك نسب الفضل لكليهما في اختراع التفاضل والتكامل. وتأتي كلمة Calculus من اللاتينية والتي تعني الحجر الصغير مشيرة إلى “الحصى” التي استُخدمت قديمًا في العد من قِبل الإغريق. ولقد كتب «ستيفن ستروغاتز-Steven Strogatz» في كتابه Infinite Powers ساخرًا أن كلا من إسحاق نيوتن وجوتفريد لايبتنز كانا يعانيان من حصوات. حيث كان يعاني نيوتن من حصوات في المثانة، ولايبتنز بحصوة في الكلى، ويالها من صدفة!
المهم أن حساب التفاضل والتكامل كان مفتاحًا للعمل على قوانين نيوتن للحركة، والتي بدورها حفزت الثورة الصناعية. كما أنها أساسية لميكانيكا الكم، التي تدعم الثورة الحديثة في أجهزة الحاسوب والاتصالات. فكان تطور حساب التفاضل والتكامل ملبيًا للحاجة الماسة لمحاولات فهم الطبيعة. أي هندسة الخطوط والأسطح المنحنية، ودراسة الكواكب والتسارع والتباطؤ في مداراتها، وقوانين التغيير وغير ذلك.
ما قبل نيوتن ولايبتنز
لكن قد سعى الكثيرون من قبل نيوتن ولايبتنز، فقد ناقشها أرخميدس في اليونان القديمة وباسكارا الثاني في الهند. وقد طورا أفكارًا لحساب التفاضل والتكامل قبل القرن ال17 بفترة طويلة. لكن لم يتم الاعتراف بأفكارهم وفهم اكتشافاتهم الثورية أو ربما دفنتها أفكار أخرى.
وفي أوائل القرن ال 17، تنافس الكثير من العلماء مثل ديكارت وبيير دي فيرما على الجمع بين الهندسة والجبر. نجم عن تلك المنافسة هندسة تحليلية ضرورية لحساب التفاضل والتكامل بالوقت الحاضر. فنحن الآن نأخذ الرسوم البيانية التي تحتوي على متغير واحد على المحور x والآخر على المحور y كأمر مسلم به. بينما لم يكن من البديهي حينذاك أنه يمكنك رسم المعادلات بهذه الطريقة.
من أين أتى مفهوم النهايات Limits؟
استخدم الإغريق طريقة الاستنفاد، وهي طريقة لإيجاد مساحة الأشكال. وقد اشتهر أرخميدس باستخدام هذه التقنية لتقدير π وإيجاد مساحة سطح الدائرة. حيث وضع أشكال ذات أضلاع مستقيمة داخل الدائرة، لكن لم تعطِ هذه الطريقة تفسيرًا لغياب حساب تلك المساحات الصغيرة جدًا على الهامش داخل الدائرة. ومن هذه النقطة بالتحديد بدأ ظهور النهايات.
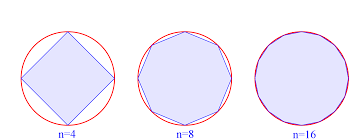
جاءت النهايات كي تعبر عن تلك المساحات الصغيرة جدًا في الهوامش، والتي مثلت مشكلة عند إيجاد مساحة أشكال كالدائرة. وهي نفس المشكلة التي عمل عليها علماء كثر وتعرف بإيجاد المماس أو المساحة تحت منحنى ما. فإذا عدنا لأرخميدس، فمهما قام بزيادة عدد الأضلاع، فستبقى هناك دائمًا مساحة صغيرة جدًا موجودة كما موضح بالصورة. ولكي تغطي الأضلاع جميع الدائرة دون أي مسافات، يجب أن تندمج نقطة البداية للضلع مع نقطة النهاية ويصبحا نقطة واحدة وذلك مستحيل رياضيًا. لأن عدد الأرقام على خط الأعداد الطبيعية لا نهائي، مهما كانت المسافة بين نقطتين صغيرة.
تلك هي نفس مشكلة الضلع الذي نود أن تتطابق نقطتيه. لذا وصل أرخميدس إلى نتيجة، وهي أن هناك رقم صغير جدًا مفقود، لكنه أكبر من الصفر. وهي نفس النتيجة التي توصل إليها أيضًا نيوتن ولايبتنز وأعطوها مصطلح «الأعداد متناهية الصغر-infinitesimal numbers». أتى العالم كوشي لاحقًا ليحل المشكلة التي ذكرناها، حيث لم يتمكن من سبقوه من حلها على نحو أدق. إذ أتى بمفهوم «النهايات-Limits». وجاء من بعده علماء مثل جورج كانتور للعمل أيضًا عليها. وتعدّ النهايات ركيزة أساسية لعلم التفاضل والتكامل بحق، فلماذا؟
إذًا ما هي النهايات Limits؟
تمثل النهاية -ويمكننا إطلاق اسم القيمة أو الحد عليها- فكرة التقارب. وتُستخدم لتعيين قيم دوال معينة في نقاط لا يمكن تحديد أي قيم فيها بالمرة. فمثلًا الدالة (x^2-1) / (x-1) غير معرفة عند x = 1. وذلك لأن القسمة على صفر ليست عملية رياضية صحيحة. لذلك، نحتاج إلى أن نعرف قيمة x التي تمكننا من تحليل البسط وقسمته على x-1 مع المقام لتجنب القسمة على الصفر، وهو ما سيعطينا x+1.
إذًا فحاصل القسمة سيساوي x+1 لجميع قيم x باستثناء 1والتي ليست لها قيمة. وعلى الرغم من ذلك، يمكننا تعيين 2 للدالة الأساسية ((x^2-1) / (x-1)) ليست كقيمتها عند x=1 لكن عندما تقترب x من 1.
وهذه هي معادلتنا الشهيرة:
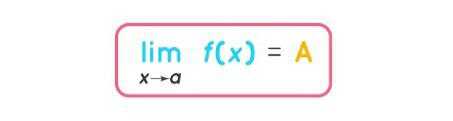
نهايةً، وجب عليك معرفة أنك لن تتمكن من الإلمام بالنهايات أو بالتفاضل والتكامل عامة بعد تلك المقدمة المبسطة بالتأكيد! لكن إليك بعض المساقات والكتب التي قد تساعد على نحو كبير في تأسيسك في هذا العلم الرائع والصعب. كما يحتاج إلى التزام وصبر، كما ننصحك بالتمارين بعد كل جزء لفهم الأفكار والتطبيقات المختلفة.
- Khan academy
- anaHr
- Thomas’ Calculus
بالاستعانة بتلك المصادر المبسطة للمبتدئين، فستفهم جيدًا. وستغنيك عن التيه بين الآلاف من المصادر التي قد تكون جيدة أيضًا.
المصادر
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.
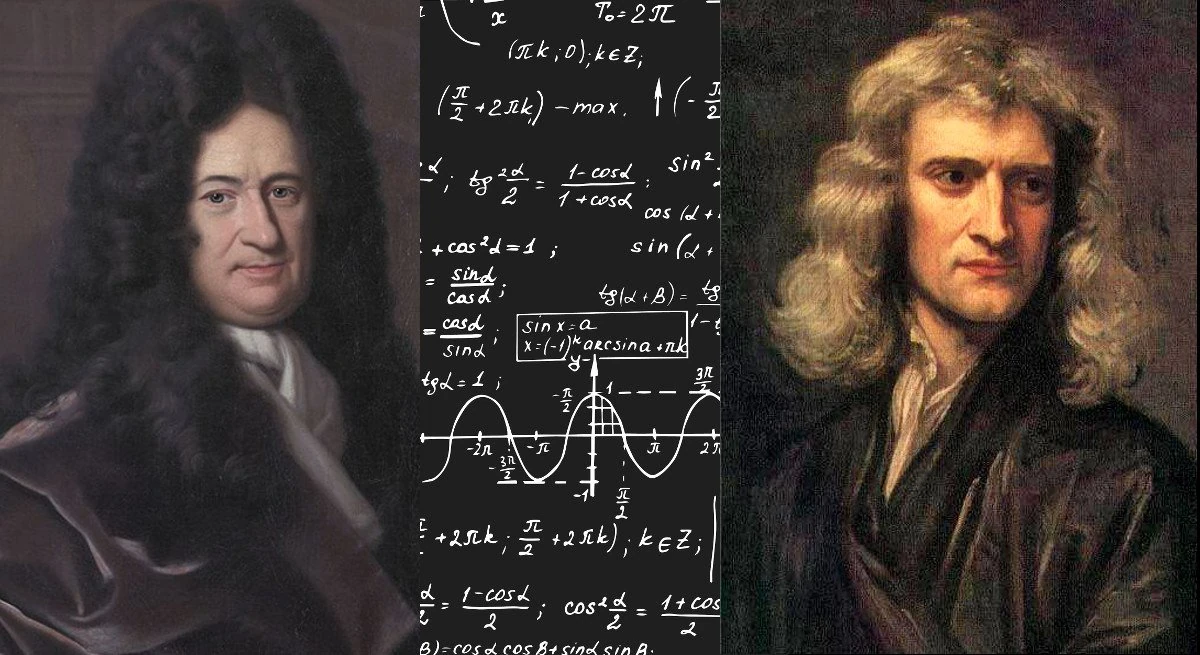


التعليقات :