ما هي حدسية بريتش-داير؟

حدد معهد كلاي للرياضيات في عام 2000 سبع مسائل في الرياضيات وقدم جائزة مالية مقدارها مليون دولار لمن يستطيع أن يقدم برهان رياضي مقبول لأي مسألة من هذه المسائل، هذه المسائل السبع هي مسألة P=NP وحدسية هودج و حدسية بوانكاريه وفرضية ريمان ونظرية يانغ-ميلز ومعادلات نافييه-ستوكس وحدسية بريتش-داير، وحتى يومنا هذا لم يستطع أحد تقديم برهان رياضي مقبول سوى لمسألة واحدة هي حدسية بوانكاريه، وفي هذه المقالة سوف نقدم شرح مبسط للإجابة على سؤال ما هي حدسية بريتش-داير؟

ما هو المنحنى الإهليجي؟

دراسة المنحنيات الإهليجية دراسة ممتدة عبر تاريخ طويل وحافل منذ القدم وحتى يومنا هذا حيث أنها متواجدة في العديد من فروع الرياضيات الحديثة، وخاصة في نظرية الأعداد، المنحنى الإهليجي هو منحنى جبري ناعم، يمكننا أن نضعة  في الصيغة الرياضية.

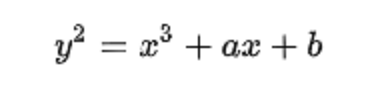
ولكي يكون المنحنى ناعماً ، لابد وأن يكون المميز الموضح في الصيغة التالية لا يساوي صفراً

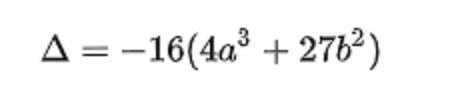
وعند وضع  a= -1 و b = 0 سيكون الناتج كما هو موضح في الصورة التالية : 

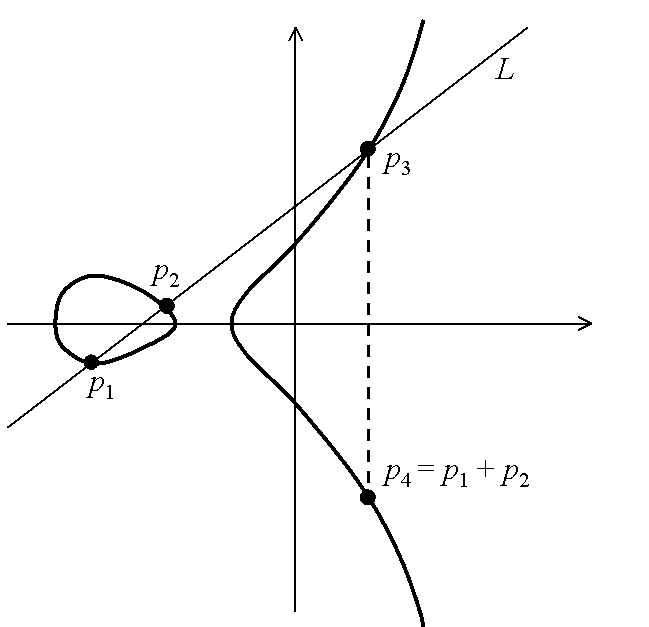
نلاحظ بأن p4=p1+p2 ، إن مجموعة النقاط الكسرية مع عملية الجمع تشكلان ما يسمى بالزمرة ، كان لويس موريديل وأندريه وايل أول من حددا بنية هذه الزمرة من النقاط الكسرية وأثمرت جهودهما بنظرية سميت باسمها، نظرية موردل- وايل في عام 1922.

ما هي حدسية بريتش-داير؟

ليومنا هذا لا توجد خوارزمية عامة ومعروفة لتحديد رتبة المنحنى الإهليجي، وإن كان هناك وسائل تطبق على بعض الحالات فقط، كما أن لكل منحنى إهليجي E  تابع عقدي بمتغير s  يعرف بالدالة اللامية  E(L،s)‎ ، اكتشف العالمان بريش وداير من خلال التجارب ما يسمى بالدالة اللامية للمنحنى الإهليجي ينص على أن درجة انعدام التابع E(L،s)‎ عند النقطة s=1  مرتبط ببعد الشبكية والموجودة في زمرة النقاط الكسرية وقد تم هذا بالتجربة وليس بالبرهان الرياضي ولذلك نطلق عليها حدسية أو فرضية ونظرا لأهمية هذه الحدسية فكانت من مسائل الألفية التي حددها معهد كلاي للرياضيات.

ما أهمية هذه الحدسية ؟

لهذه الحدسية ميزة رائعة حيث تربط بين عالم الجبر حيث معادلات كثيرات الحدود وعالم التوابع العقدية حيث تنتمي الدالة اللامية ولا عجب أنها ساهمت في تطوير نظرية الأعداد.

المصادر

1ـ Claymath

2ـ Theconversation

3ـ Brilliant

Author: Nader Elshebli