ما هي نظرية فيثاغورث وما تطبيقاتها؟
كنت خارج المنزل ونسيت المفتاح بالداخل ويوجد نافذة وحيدة مفتوحة في الطابق الثاني على ارتفاع 25 قدمًا فوق سطح الأرض. لابد لك أن تستعير سُلم من أحد جيرانك ويوجد شجيرة على حافة منزلك؛ لذا سيكون عليك وضع السلم على بعد عشرة أقدام من المنزل. فما طول السلم الذي تحتاجه للوصول إلى النافذة؟
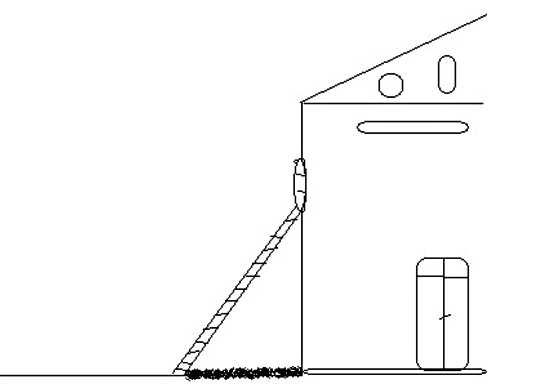
لمعرفة طول السلم، ما عليك سوى استخدام قانون فيثاغورث الذي بالتأكيد قد درسته في إحدى مراحلك الدراسية. في هذه المقالة ستتعرف على ما هي نظرية فيثاغورث وما تطبيقاتها؟ بالتفصيل -وهذه المقالة هي الأولى من سلسلة أشهر المعادلات الرياضية-، فهيا بنا لنتعرف على أولى معادلتنا الشهيرة.
محتويات المقال :
فيثاغورث ليس رياضيًّا فقط
وُلد فيثاغورث في ساموس باليونان في 570 قبل الميلاد، وتوفي حوالي (500-490) قبل الميلاد. ذهب إلى مصر وبابل في شبابه وهاجر إلى جنوب إيطاليا تقريبًا في 532 قبل الميلاد -غالبًا هربًا من الحكم المستبد في ساموس- وأسس مدرسته في كروتون بإيطاليا ومن ثم فر منها إلى ميتابونتو بإيطاليا حيث توفي.
قيّل أنه أول عالم رياضيات اقترح أن كل شيء تمثله الأرقام. وعلى الرغم من أنه اشتهر عن طريق الرياضيات بنظريته الشهيرة، إلا أنه حقق إنجازات غير عادية في علم الفلك؛ فأدى اهتمامه بالفلك -كما هو الحال مع العديد من الإغريق قديمًا- مع فهمه العميق للأرقام إلى تأكيد أن الأرض عبارة عن كرة. كذلك كان يرى فيثاغورث أن كل من الرياضيات والموسيقى مترابطتين، وكان يعتقد أن للموسيقى خصائص علاجية. إضافةً إلى أنه ساهم في تطور نظرية الموسيقى. كما كان لأكاديميته في كروتون بإيطاليا تأثير في فكر أفلاطون وأرسطو…
ما هي نظرية فيثاغورث؟
هي نظرية هندسية شهيرة، إذ تشرح العلاقة بين أضلاع المثلث القائم الزاوية -وتسمى أضلاع المثلث القائم الزاوية أيضًا بثلاثيات فيثاغورث-. وعلى الرغم من ارتباط النظرية بالعالم فيثاغورث إلا أنها قديمة، حيث اكتُشتف النظرية على ألواح بابلية بين 1600 و1900 قبل الميلاد وذلك من قبل فيثاغورث وكذلك ذُكرت النظرية في الهند مكتوبة بين 800 و400 قبل الميلاد. لكن يقترح العلماء بأنه ربما تلك الاكتشافات كانت كلا منها على نحو مستقل في العديد من الثقافات المختلفة.
بيان نظرية فيثاغورث
تنص النظرية على أن “مربع طول الوتر (الضلع الطويل) يساوي مجموع مربعات الضلعين الآخرين (ضلعي الزاوية القائمة)”. فتوضع أضلاع المثلث القائم الزاوية (أ ب ج) والتي لها قيم صحيحة موجبة في معادلة تسمى ثلاثية فيثاغورث.
حيث أ الضلع العمودي وب ضلع القاعدة وج هو الوتر وتكون العلاقة هكذا:
أ² + ب² = ج²
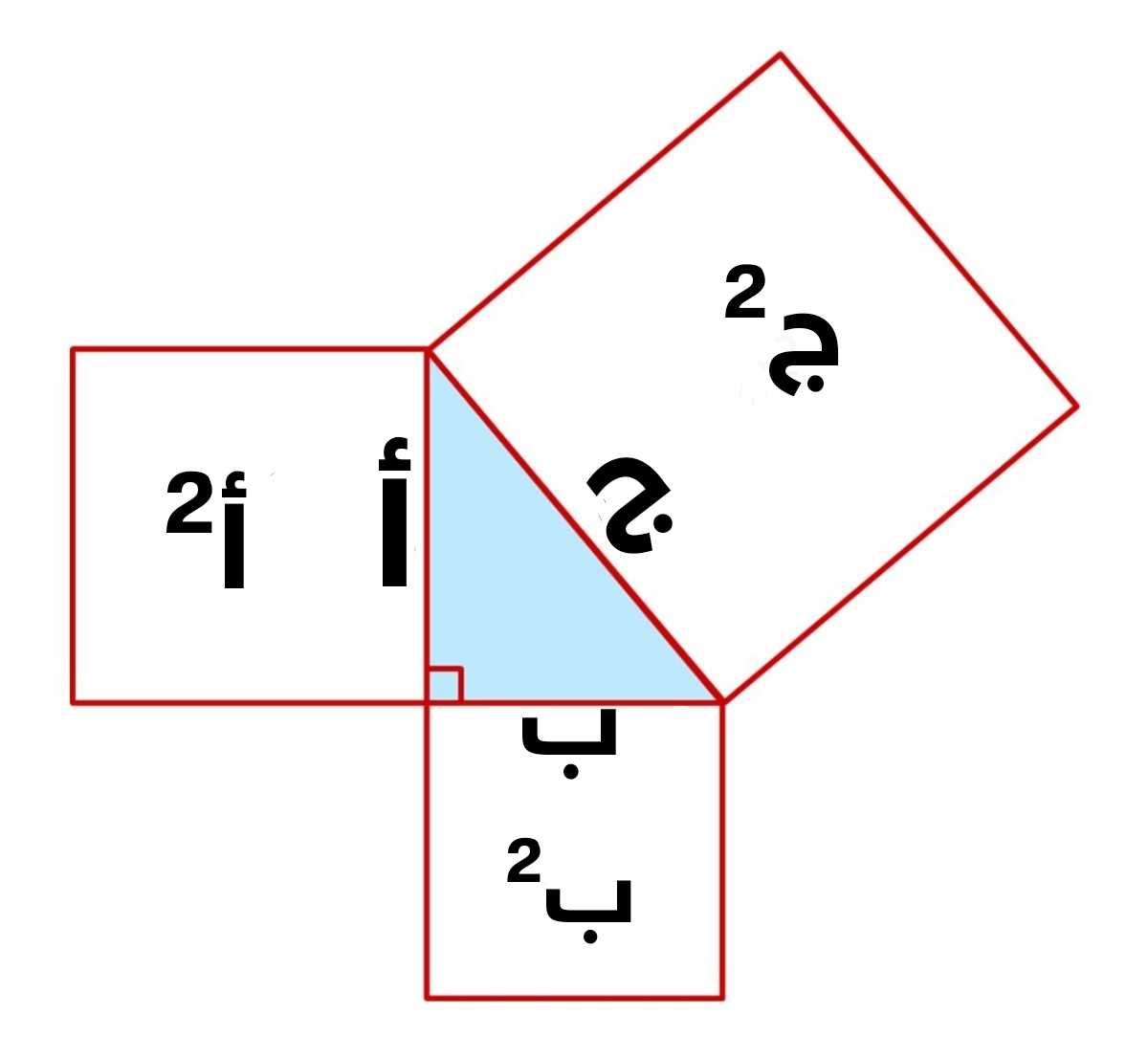
إثبات نظرية فيثاغورث
من الشكل التالي، مساحة المربع الداخلي هي: ج × ج = ج²
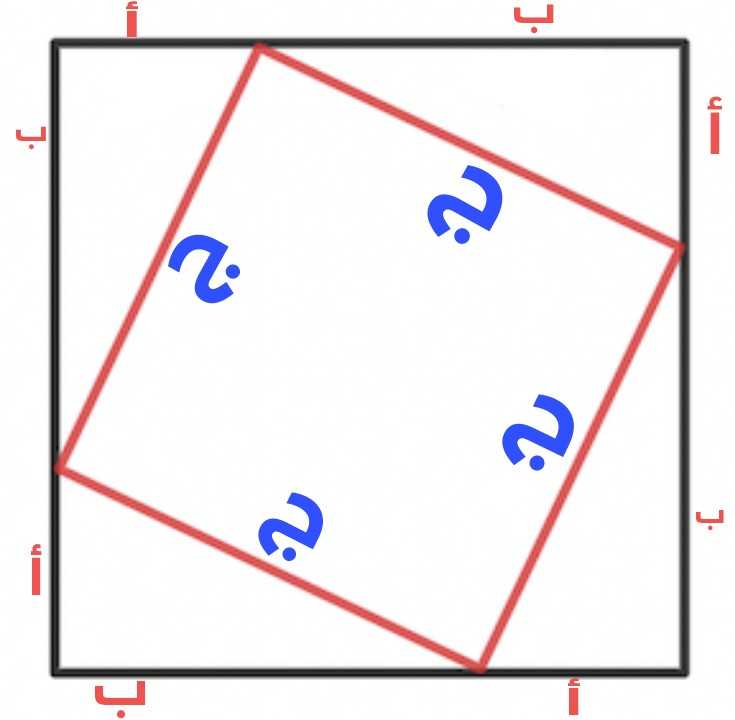
ومساحة المربع الخارجي تكون:
(أ + ب)² = أ² + ب² + 2 أب
قد نجد مساحة المربع الخارجي هكذا:
مساحة المربع الخارجي = مساحة المربع الداخلي + مجموع مساحات المثلثات الأربعة القائمة حول المربع الداخلي وستكون:
أ² + ب² + 2 أب = ج² + 4•1/2 أب
ونستنتج من المعادلة الأخيرة أن: أ² + ب² = ج²
(هذا إثبات من إثباتات عديدة للنظرية).
عكس نظرية فيثاغورث
تنص عكس النظرية على أنه “إذا كان مربع أحد الأضلاع يساوي مجموع مربع الضعلين الآخرين، فيجب أن يكون المثلث قائم الزاوية”.
إثبات عكس نظرية فيثاغورث
علمنا أنه النظرية تنص على:
أ² + ب² = ج²
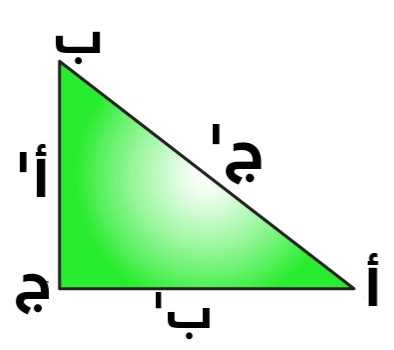
وبفرض المثلث ه و د أدناه، حيث أ ج = ه د، ب ج = و د. باستخدام معادلة فيثاغورث ينتج أن:
(ه و)² = (و د)² + (ه د)² = ب’² + أ’² >>> (1)
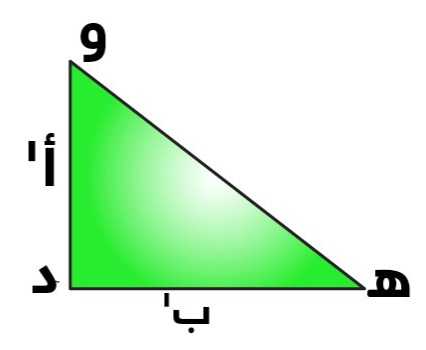
ومن المثلث أ ب ج، باستخدام فيثاغورث ينتج أن:
(أ ب)² = (ب ج)² + (أ ج)² = ب’² + أ’² >>> (2)
من معادلة 1, 2، ينتج أن:
(ه و)² = (أ ب)²، إذًا ه و = أ ب.
وينتج عن ذلك أن المثلثين متطابقين وزاوية د (ه د و) هي زاوية قائمة.
تطبيقات نظرية فيثاغورث
يمكننا رؤية تطبيقات تلك النظرية في حياتنا اليومية -كما ذكرنا مثال في بداية المقالة- وفي شتى المجالات المختلفة وإليكم بعض الأمثلة:
المجالات الهندسية والإنشائية
يستخدم معظم المهندسين المعماريين النظرية للعثور على الأبعاد غير المعروفة، عندما يكون الطول والعرض معروفين؛ بذلك يكون من السهل حساب قطر قطاع معين. فتُستخدم بشكل رئيس في بعدين في المجالات الهندسية.
تُطبق نظرية فيثاغورث في التصميم الداخلي والهندسة المعمارية للمنازل والمباني.
الكاميرات الأمنية
تستخدم ميزة التعرف على الوجوه في الكاميرات الأمنية النظرية، بحساب المسافة بين الكاميرا وموقع الشخص.
الملاحة
يستخدم الأشخاص المسافرين عبر البحر نظرية فيثاغورث للعثور على أقصر مسافة أحيانًا للوصول لوجهتهم المعنية.
الطب
اعتمد علماء الأوبئة المنحنيات لمساعدتهم على تحديد النقطة التي يتعافي فيها الفرد من المرض وقد اتفقوا على أن النقطة الصحيحة للاختيار هي الأقرب للزاويا العلوية اليسرى ويتم استخدام النظرية في تحديد تلك النقطة.
فتطبيقات نظرية فيثاغورث لا تُعد ولا تحصى وستجد أهميتها في كل شيء حولك.
المصادر
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.



التعليقات :