سلسلة تعلم الخوارزميات: ما هي الخوارزميات التراجعية Backtracking Algorithms ؟
تُعدُّ الخوارزميات التراجعية إحدى نماذج الخوارزميات التي تعمل على تجريب كل الحلول الممكنة لحل مشكلة أو مسألة ما بحيث تتميز تلك المسألة بعدم القدرة على الحل إلا بتجربة كل حل ويُجرب كل حل مرة واحدة فقط وتُزال تلك الحلول التي تفشل في تلبية قيود المشكلة وتحقيق نتيجة مناسبة.
على سبيل المثال، الهدف من لعبة سودوكو هو ملء كل المربعات بالأرقام مع الأخذ بالاعتبار عدم تكرار أي رقم في أي صف أو عمود.
ما يقوم به اللاعب المحترف للعبة سودوكو هو محاولة ملء كل المربعات رقمًا برقمٍ وعندما يجد أن الرقم الحالي لا يمكن أن يؤدي إلى حل يقوم بإزالته أو بمعنى آخر “يتراجع” عن هذا الرقم ويجرب رقمًا آخر. هذه الطريقة أفضل من حساب كل المجموعات الممكنة من الأرقام ثم تجربة كل مجموعة واحدة تلو الأخرى.
مثال آخر لاستخدام الخوارزميات التراجعية هو حل مسائل المتاهات إذ نجرب كل الطرق الممكنة للخروج من المتاهة فإذا وجدنا الطريق مفتوحًا نكمل في هذا المسار وإن وجدناه مسدوداً نقوم بالرجوع خطوة إلى الوراء ونجرب مسارًا آخر وهكذا حتى نصل إلى نقطة الخروج.
يشير مصطلح التراجع إلى أنه إذا لم يكن الحل الحالي مناسبًا، فعليك التراجع وتجريب الحلول الأخرى. يستخدم هذا النهج في حل المشكلات التي لها حلول متعددة. أما إذا أردنا حلًا مثاليًا- كإيجاد أقصر الطرق للخروج من المتاهة- فيجب علينا حينها استخدام خوارزميات البرمجة الديناميكية كما أسلفنا ذكره في المقال السابق.
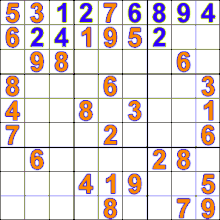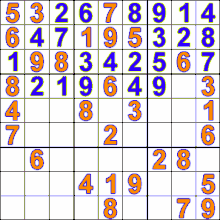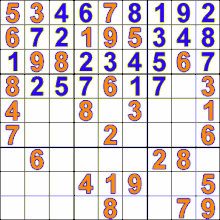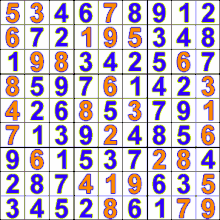
ملء المربعات بالأرقام في لعبة سودوكو باستخدام الخوارزميات التراجعية Backtracking Algorithms
محتويات المقال :
استخدام شجرة فضاء الحالة لتمثيل حالات المسائل
تُستخدم شجرة فضاء الحالة «State Space Tree» لتمثيل جميع الحالات الممكنة للمسألة أو للمشكلة بحيث يمثل جذر هذه الشجرة الحالة الأولية بينما تعبر أوراقها عن الحالة النهائية للمسالة.
تجدر الإشارة إلى أن المقصود بمصطلح «الحالات الممكنة للمسألة-the possible states» أنها المسارات التي تؤدي إلى حل أو إلى عدم حل للمسألة. ويساعد استخدام شجرة فضاء الحالة في استيعاب المسائل بشكل مرئيٍ وواضح.
لتوضيح مفهوم شجرة فضاء الحالة واستخدامها في تمثيل الخوارزميات التراجعية تابع معنا المثال الآتي: لنفترض أننا نريد أن نحسب كل الطرق الممكنة لترتيب ولدين وفتاة واحدة على 3 مقاعد مع مراعاة ألا تكون الفتاة على المقعد الأوسط. سنستخدم الموز التالية لتسهيل التعامل مع المسالة: الولد الأول B1 والولد الثاني B2 والفتاة G.
بعد ذلك سنستخدم هذه الرموز لتمثيل جذر شجرة فضاء الحالة وفي كل فرع سنجرب كل الاحتمالات الناقصة فمثلا في الفرع الذي يوجد به الولد الأول سيتفرع منه فرعان أحدهما يمثل البنت والآخر يمثل الولد الثاني وعند هذه النقطة سنتفحص قيود المسألة مجددًا وهي عدم وجود البنت في المقعد الأوسط لذا لن يتفرع من الفرع الذي يمثل البنت أي فرع آخر في هذه الحالة لأنه مخالف لشروط المسألة وهكذا بالنسبة لبقية الحالات.
تفحّص الصورة أدناه جيدًا لاستيعاب مفهوم التراجع عن الحل أو الخوارزميات التراجعية.
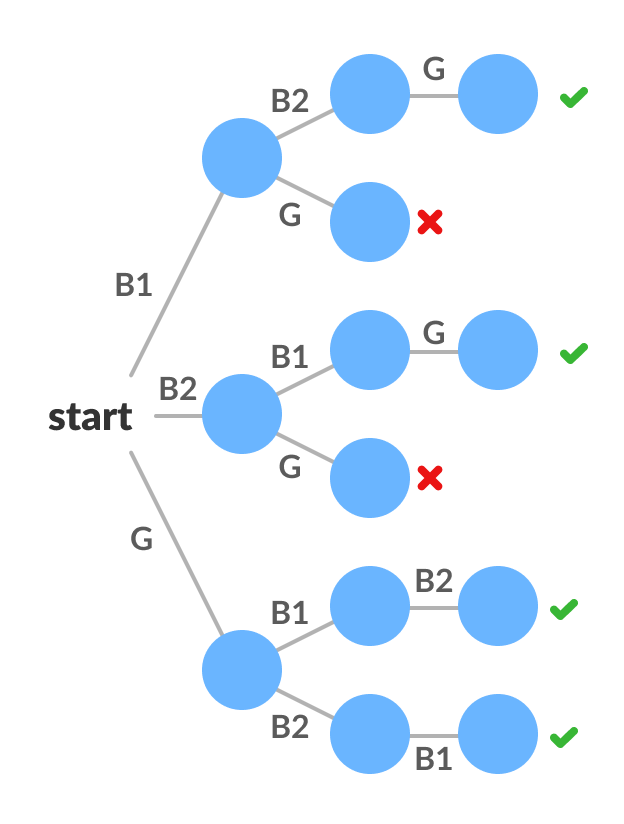
شجرة فضاء الحالة لمسالة ترتيب ولدين وفتاة
مسألة الوزراء الثمانية في الشطرنج
يُعد الوزير القطعة الأقوى في لعبة الشطرنج إذ يستطيع التحرك في ثماني اتجاهات إلى الأعلى والأسفل وإلى اليمين والشمال بالإضافة إلى الاتجاه المحوري أو القطري لمسافات غير محدودة وهذا ما يجعل مسألة وضع ثمانية وزراء على رقعة الشطرنج بحيث لا يهدد أي منهم الآخر أمر بالغ التعقيد. ولكي تتصور صعوبة هذه المسألة عزيزي القارئ يكفي أن تعرف أن هنالك 4,426,165,368 طريقة لوضع الثمانية الوزراء في رقعة الشطرنج- إذا تكاسلت عن قراءة الرقم فهو يُقارب 4 مليار ونصف-.
التحدي الأكبر هنا هو البحث عن الطرق التي تفي فقط بمتطلبات المسألة أي الطرق التي يمكن فيها وضع 8 وزارء في رقعة الشطرنج بحيث لا يهدد أحد منهم الآخر.
من هنا تأتي أهمية الخوارزميات التراجعية في تقليص عدد الطرق الممكنة لحل لغز الوزراء الثمانية إذ سنقوم باستبعاد أي طريقة لا تؤدي على الحل فمثلًا عند وضع وزيرين فقط على القطعة سننظر هل يهدد أحدهما الآخر؟ فإن كان كذلك فإننا سنقوم باستبعاد هذا الحل ولن نمضي قدمًا في اختبار بقية الوزراء الستة وهكذا وبالتالي سنجد فقط 92 طريقة ممكنة فقط لوضع الوزراء الثمانية مع الالتزام بقيد المسألة وإذا قمنا باستبعاد التدوير والانعكاس لرقعة الشطرنج فسيتقلص عدد الحلول إلى 12 حلًا فقط ويطلق عليهم اسم الحلول الأساسية للغز الوزراء الثمانية.
بالطبع لحل مثل هذه المسائل سنحتاج إلى أجهزة حاسوب ذات قدرة حاسوبية عالية للتوصل إلى الحل بشكل أسرع مقارنة بالحل اليدوي.
أخيرًا قد تتساءل عن الكيفية التي تم عن طريقها حساب الطرق الممكنة لوضع الوزراء الثمانية في قطعة الشطرنج والجواب هو باستخدام ما يعرف بالرياضيات باسم التوافيق.
بمعنى آخر، لدينا 64 مربع في رقعة الشطرنج ولدينا 8 وزراء ووفقًا لقاعدة التوافيق فإن العدد الكلي للطرق يساوي حاصل قسمة مضروب العدد 64 على حاصل ضرب مضروبي العددين 8 و 56 والعدد 56 هو ناتج الفرق بين 64 و 8 ويمثل رياضيًا كالتالي:
(64C8) = 64!/56 ! x 8!
لمعرفة كيفية حساب مضروب العدد «factorial» راجع مقال الخوارزميات العودية بالضغط هنا .
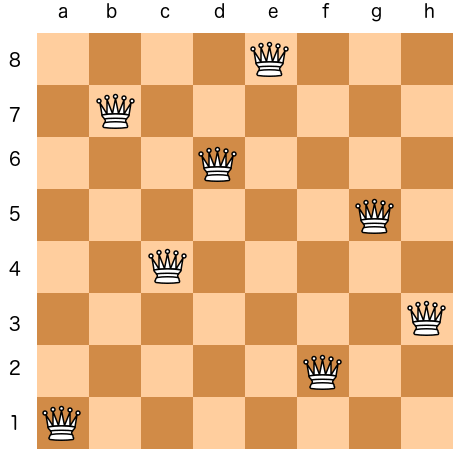
أحد حلول مسألة الوزراء الثمانية
المصادر
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.



التعليقات :