دليلك لفهم خوارزمية أدم ADAM التحسينية الأكثر استخدامًا في التعلم العميق

اختيارك للخوارزمية التحسينية المناسبة لتدريب نموذجك للتعلم العميق، يعني مباشرة اختيارك جودة ومدة التنفيذ. فاختيارك هذا له الكلمة الفصل في قدرتك على الحصول على نتائج في دقائق، أو ساعات، أو حتى أيام. أو ربما عدم حصولك على نتيجة خلال فترة حياتك. ومن بين هذه الخوارزميات، نجد أن خوارزمية أدم ADAM هي أحد أكثر الخوارزميات التحسينية استخدامًا في مجال التعلم العميق. وتحديدًا في تدريب الشبكات العصبية الاصطناعية. وقد أشرنا سابقا أن خوارزمية النزول التدرجي ومتحوراتها هم الأكثر استخدامًا في هذا المجال، لكن ما لم نذكره هو أن خوارزمية أدم ADAM هي متحور من متحورات خوارزمية النزول التدرجي. وبالتحديد خوارزمية النزول التدرجي التصادفية Stochastic Gradient descent.

وقد استخدمت خوارزمية النزول التدرجي التصادفية SGD في السنوات الأخيرة بشكل مكثف وكبير في فروع عديدة من الذكاء الاصطناعي، لعل أبرزها هما الرؤية الحاسوبية computer vision، ومعالجة اللغة الطبيعية Natural Language Processing.

ما هي خوارزمية أدم ADAM؟

أصول خوارزمية أدم ADAM

ابتُكرت خوارزمية أدم بهدف استبدال خوارزمية النزول التدرجي التصادفية، وذلك، تحديداً في عملية تدريب نماذج التعلم العميق deep learning. وقد تم اقتراح هذه الخوارزمية من طرف دايديريك كينغما Diederik Kingma رائدة المجال OpenAI و جيمي با Jimmy Ba من جامعة تورونتو سنة 2015 في ورقة بحثية في مؤتمر ICLR باسم “أدم: طريقة للتحسين التصادفي”، Adam: a method for stochastic optimization. تم تسمية هذه الخوارزمية أدم اختصارًا ل: ADAptive Moment estimation <=> ADAM.

مميزات الخوارزمية

في تقديمهم لخوارزمية أدم، وضح الباحثان مميزات هذه الخوارزمية في التعامل مع المشاكل غير المحدبة، أي دالتها الهدف غير محدبة non-convex objective function. من بينها:

• سهولة تنفيذ الخوارزمية.
• كفؤة حوسبيًا computationally efficient.
• استهلاك ضعيف للذاكرة.
• غير حساسة لإعادة القياس القطري للتدرجات. أي أنها غير حساسة لضرب متجهة التدرج في مصفوفة قطرية موجبة العوامل. لكونها تستعمل المشتقات الجزئية، بدلًا من التدرج الذي تستعمله خوارزمية النزول التدرجي التصادفية.
• منسابة عند تعدد المتغيرات وكبر عينات البيانات.
• جيدة مع المشاكل غير الثابتة، أي فضاء البحث متغير بدلالة الزمن.
• فعالة عند وجود تشويش يؤثر على قيم التدرج.
• المتغيرات الأساسية في التحكم في التنفيذ، أي المعلمات الفائقة hyperparameters، بديهية ولا تحتاج ضبط معقد. وضبط هذه الأخيرة parameter tuning يعد مشكلةً تحسينيةً هو الأخر، ونستعمل خوارزميات تحسينية لضبطها عند الحاجة.

آلية عمل أدم

تختلف أدم عن خوارزمية النزول التدرجي التصادفية. لكونها تأخذ معدل تعلم بارامتري، أي معدل تعلم يتغير بدلالة متغيرات معينة. معدل التعلم هذا هو حجم الخطوة عند كل دورة تكرار تقليص للدالة الهدف. راجع(ي) المقال السابق لتوضيح أكبر: تعرف على خوارزمية النزول التدرجي الأشهر في الخوارزميات التحسينية.

يتم تحديد معدل التعلم، أو حجم الخطوة هذا، انطلاقا من تقديرات العزم الأول والثاني للتدرج. فيصف الباحثان هذه الخوارزمية بكونها دمجًا بين إثنتين من سابقتيها، واللتان بدورهما من متحورات خوارزمية النزول التدرجي التصادفية وهما:

خوارزمية التدرج المتأقلم

Adaptive Gradient Algorithm، أو AdaGrad: والتي هي الأخرى تستعمل حجم خطوة متغير لتعزيز أدائها في حل المشاكل ذات التدرج الضئيل. ما يعني في التعلم العميق أن الشبكة لا تستقبل إشارات كافية لضبط أوزانها. ومن أمثلة هذه المشاكل نجد: معالجة اللغة الطبيعية NLP، و الرؤية الحاسوبية، وغيرها.

خوارزمية انتشار جذر متوسط المربع

Root Mean Square Propagation، أو RMSPropa: التي أيضًا تستعمل خطوة متغيرة. ذلك التغير، بدلالة متوسط مُضمحل للتدرجات الجزئية. ما يعني أن أداء هذه الخوارزمية جيد عند مواجهتها لمشاكل ذات فضاء بحث متغير زمنيًا، أو عند وجود تشويش يغير من قيم التدرج.

كيف تجمع أدم ADAM فوائد هاتين الخوارزميتين؟

فبدلاً من تكييف معدلات التعلم لمتغيرات الدالة الهدف بناءً على متوسط ​​العزم الأول average first moment كما هو الحال في RMSProp، تستخدم آدم أيضا متوسط ​​العزوم الثانية للتدرجات Uncentered variance.

وباستعمال العزم فإننا نتمكن من التحكم في مقدار النزول التدرجي بطريقة تكون فيها التذبذبات عند أدنى قيمها عند اقترابنا للحل الأمثل، أي تقلص حجم الخطوات كلما أصبحنا أقرب للحل الأمثل. بينما يكون حجم الخطوة معتبرًا عند اقترابنا لحل محلي.

رياضيات

العزم

يستعمل العزم لتسريع النزول التدرجي.

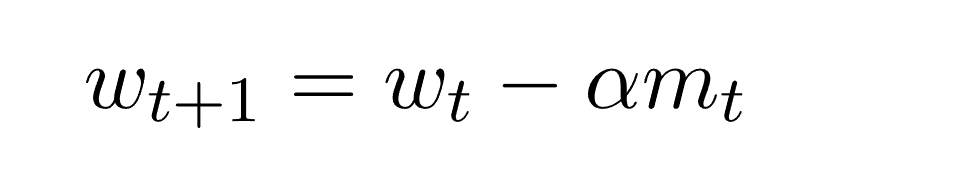
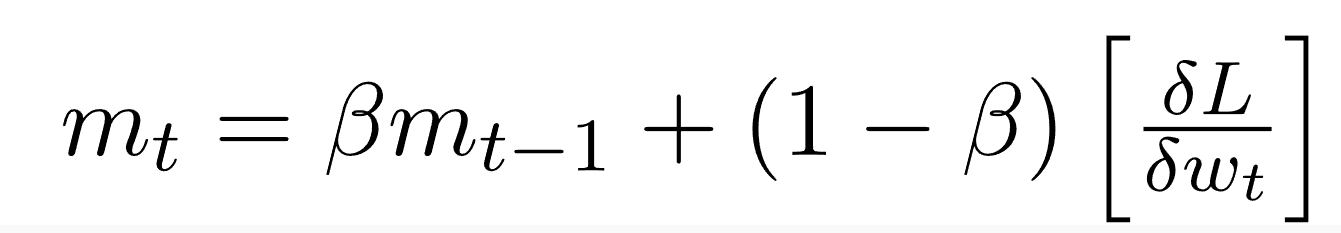
انتشار جدر متوسط المربع RMSProp

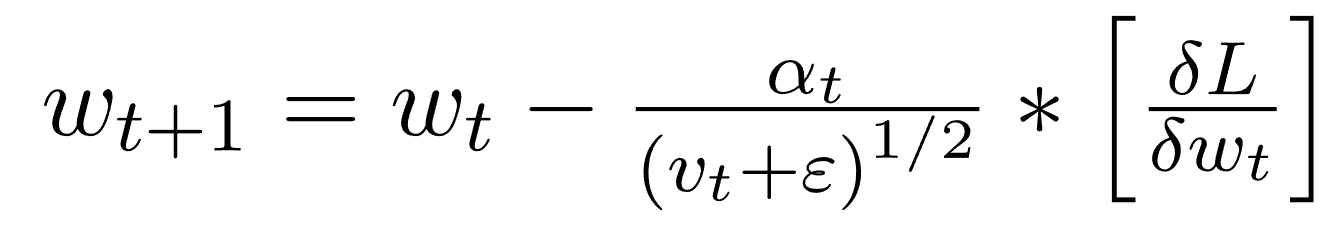
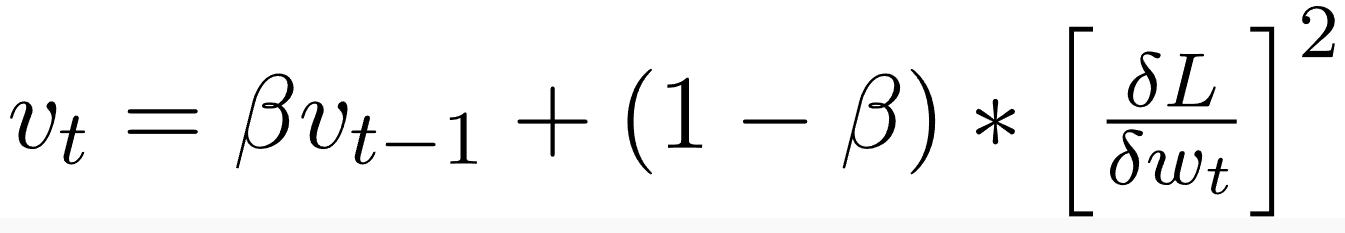
أدم

انطلاقا من معادلات الطريقتين أعلاه، نتحصل على:

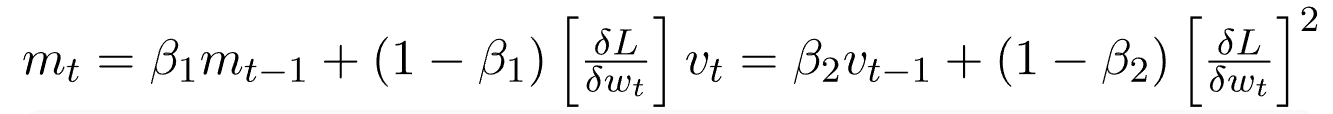
نظرًا لأن كل من mt و vt قد تم تصفيرهما بدئيًا، وكذلك لكون β1 و β2 تأخد قيم تقارب 1، لوحظ تجريبيًا أنهما يكتسبان تحيزًا نحو الصفر. لإصلاح هذا نقوم بحساب قيم تصحيحية. ويتم حساب هذه القيم أيضًا للتحكم في الأوزان عند قرب وصولنا للحل الأمثل وذلك لمنع التذبذبات عالية التردد. والصيغ المستخدمة هي:

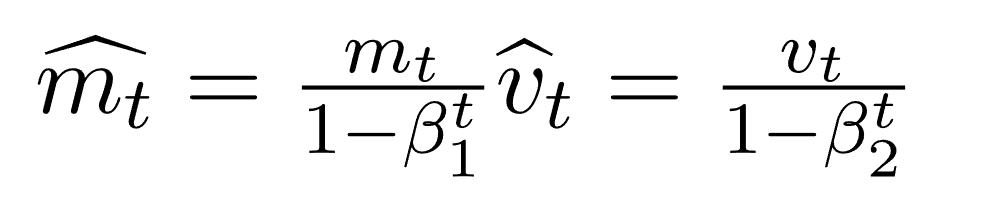
ما يمكننا من استبدال mt و vt بقيم مصححة:

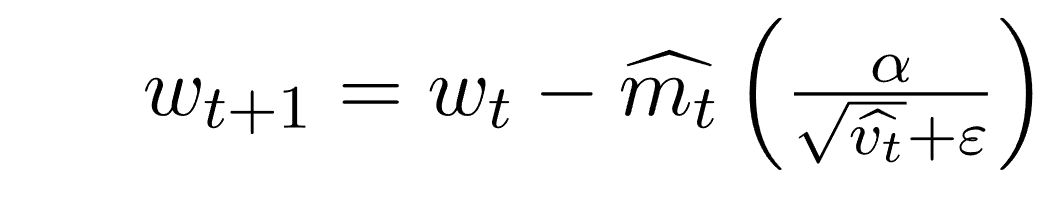
الأداء العملي

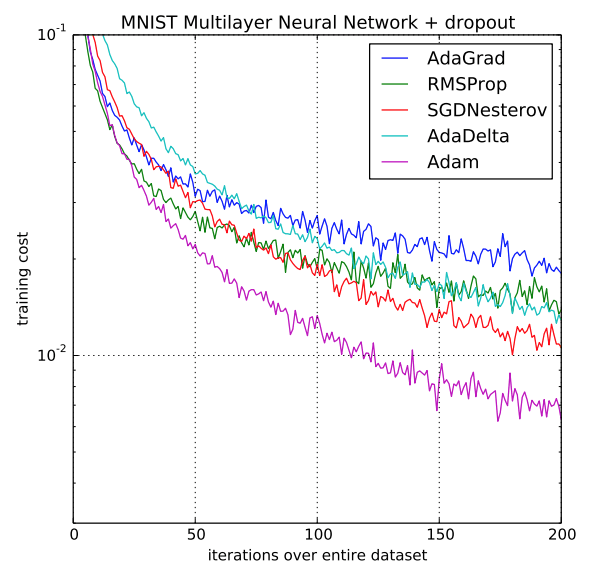
لكونها مبنية على نقاط قوة سابقاتها، فإن خوارزمية أدم ADAM هي أحد أفضل الخوارزميات التحسينية على الإطلاق، وذلك إن لم تكن أصلا أفضلها. فنجد أن هذه الخوارزمية تقدم أداء أعلى بهامش كبير من أداء نظيراتها، بحيث تتفوق عليهم لا من حيث كلفة تدريب النماذج فقط بل ومن حيث الأداء السريع والعالي.

مصادر

1. MachineLearningMastery
2. GeeksforGeeks
3. Cornell