سلسلة تعلم الخوارزميات: ما هي خوارزميات البرمجة الديناميكية؟ تُعرف خوارزميات البرمجة الديناميكية بأنها طريقة حل مشكلة معقدة عن طريق تقسيمها إلى مجموعة من المشاكل الفرعية الأبسط، وحل كل مشكلة فرعية مرة واحدة فقط وتخزين حلولها باستخدام بنية بيانات قائمة على الذاكرة كالمصفوفة أو الخريطة مثلًا. ومن ثم فهرسة كل حل من حلول المشكلة الفرعية بطريقة ما بناءً على قيم معلمات الإدخال الخاصة به وذلك لتسهيل البحث.
لذلك في المرة التالية التي تحدث فيها نفس المشكلة الفرعية، بدلاً من إعادة حساب حلها، يبحث المرء أو الحاسوب ببساطة عن الحل المحسوب مسبقًا وبالتالي توفير وقت الحساب. لتقريب مفهوم خوارزميات البرمجة الديناميكية أكثر تخيل أن شخصًا ما طلب منك حساب مجموع 1+1+1+1+1+1 فبعد أن تقوم بالحساب ستقول له ان الإجابة هي 6. الآن إذا طلب منك +1 للسؤال السابق وطلب منك الإجابة بسرعة فم الذي ستقوم به؟
بالتأكيد لن تقوم بالحساب من جديد لأنك لا زلت تتذكر الجواب السابق وبالتالي ستقوم بإضافة الرقم 1 للجواب السابق 6 وستكون إجابتك للسؤال الجديد هو 7 وهذا بالضبط ما تقوم به خوارزميات البرمجة الديناميكية إذ تُخزن النتائج التي نحصل عليها من المسائل الفرعية وبهذا تنتفي الحاجة إلى إعادة حساب تلك النتائج في وقت لاحق.
محتويات المقال :
كيفية حل مسائل البرمجة الديناميكية؟
يمكن تلخيص خطوات حل مسائل البرمجة الديناميكية كالتالي:
- تحديد إذا ما كانت المسألة ذات طبيعة برمجة ديناميكية أم لا: بشكل عام، يمكن حل جميع المشكلات او المسائل التي تتطلب تعظيم أو تقليل كمية معينة أو مشاكل العد التي تنص على حساب الترتيبات في ظل ظروف معينة أو المسائل الاحتمالية باستخدام البرمجة الديناميكية. بالإضافة، تلبي جميع مسائل البرمجة الديناميكية خاصية المسائل الفرعية المتداخلة، كما أن معظم المسائل الديناميكية التقليدية تلبي أيضًا خاصية البنية الفرعية المثلى أي أنه بالإمكان الحصول على الحل المثالي للمسألة المعطاة بجمع الحلول المثالية للمسائل المتفرّعة عن المسألة الرئيسية وبمجرد ملاحظة هذه الخصائص في مسألة معينة، تأكد من أنه يمكن حلها باستخدام خوارزميات البرمجة الديناميكية
- تحديد مقدار انتقال الحالة: بعد التأكد من أن المسألة يمكن حلها بواسطة البرمجة الديناميكية تأتي خطوة تحديد مقار انتقال الحالة. تُعرف الحالة على أنها مجموعة من المعلمات التي يمكن أن تحدد بشكل فريد موقفًا معينًا في مشكلة معينة. يجب أن تكون مجموعة المعلمات هذه صغيرة قدر الإمكان لتقليل مساحة الحالة ونوضحها لاحقًا بمثال تطبيقي.
- صياغة العلاقة بين الحالات: بعد أن نحدد مقدار انتقال الحالة تأتي خطوة تحديد العلاقة التي تربط بين الحالات السابقة والحالات الحالية وتُعد هذه الخطوة من أصعب الخطوات التي يمكن أن يواجهها المبرمج أثناء حل مسائل البرمجة الديناميكية.
- إضافة التحفيظ أو الجدولة إلى الحالة: وفي هذه الخطوة تُخزّن الإجابة عن حالة معيّنة في جدول البحث وذلك لاستدعائها مرة أخرى إن تطلب الأمر ذلك دون الحاجة إلى حسابها مرة أخرى. عند استخدام طريقة التحفيظ، في كل مرّة نحتاج فيها إلى إيجاد حلٍّ لمسألة فرعية، نبدأ بالبحث في جدول البحث، فإن كانت القيمة محسوبة مسبقًا موجودة فيه فسنعيد حينئذٍ تلك القيمة، وإلا سنحسب القيمة ونضع النتيجة في جدول البحث ليتسنى لنا إعادة استخدامها في وقت لاحق. سنقوم بتوضيح هذه الخطوات في مثال مسألة حقيبة الظهر.
مسألة حقيبة الظهر «The knapsack problem»
تنتمي مسألة حقيبة الظهر إلى فئة من مسائل “NP”، والتي تعني “زمن كثيرة الحدود غير الحتمية” ويُشير هذا الاسم إلى الكيفية التي تجبر بها هذه المسائلُ جهاز الحاسوب على المرور بالعديد من الخطوات للوصول إلى حل، ويزداد العدد بشكل كبير بناءً على حجم المدخلات. لتبسيط مفهوم مسألة حقيبة الظهر، لنفترض أنك بصدد السفر إلى منطقة ما لزيارة أصدقائك ولديك العديد من الهدايا في داخل حقيبتك ولكن شركة الطيران تسمح لك بحمل وزن معين فقط ولا يجب أن تتعداه فقررت في هذه الحالة تعبئة الحقيبة بعدد معين من الهدايا بحيث تمثل أكبر قيمة ولا تتعدى وزنها الحد المسموح به من الوزن بعبارة أخرى نعبئها بما خف وزنه وغلا ثمنه.
من الواضح في البداية أنَّ ما يجب فعله هو اختبار كل المجموعات الممكنة، وحساب قيمتها ووزنها، ثم اختيار المجموعة التي تحقق الحد المقبول للوزن والحد الأقصى للقيمة. هذا يفي بالغرض إذا كان عدد العناصر قليلا، لكن الأمر يصبح أصعب مع عدد كبير منها ولتوضيح صعوبة الأمر دعنا نبدأ بالمثال التالي: افترض أن لديك في الحقيبة خمسة عناصر والمطلوب منك اختيار العناصر التي تحقق أعلى قيمة وفي الوقت ذاته لا يتجاوز وزنها الحد المسموح به وهو 10 كيلو جرام وكانت العناصر كالتالي: العنصر الأول قيمته 5 دولار ووزنه 4 كيلو جرام.
العنصر الثاني قيمته 10 دولار ووزنه 8 كيلو جرام. العنصر الثالث قيمته 3 دولار ووزنه 3 كيلو جرام. العنصر الرابع قيمته 2 دولار ووزنه 5 كيلو جرام والعنصر الخامس قيمته 3 دولار ووزنه 2 كيلو جرام. بعد القليل من التفكير ستجد أن العنصر الثاني والعنصر الخامس هما أفضل عنصران يحققان أعلى قيمة (13 دولار) وفي الوقت ذاته لا يتجاوزان الوزن المسموح (10 كيلو جرام).
الآن، ماذا لو كان عدد العناصر كبيرًا للغاية؟ إذا استخدمت الطريقة التقليدية للحل ستسهلك الكثير من الوقت لمعرفة مجموعة العناصر التي تحقق شرطي القيمة المثلى والوزن المسموح به بمعنى اخر لو كان لديك 10 عناصر فإن عدد المجموعات الفرعية التي ستقوم بفحصها هو 1024 مجموعة فرعية ومن ثم ستقوم باختيار أنسب مجموع تحقق الشرطين السابقين.
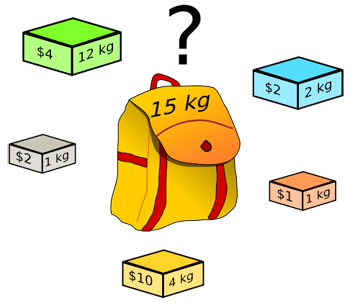
حل مسألة حقيبة الظهر بواسطة خوارزمية البرمجة الديناميكية
تحقق مسألة حقيبة الظهر شرط البرمجة الديناميكية إذ أنه بالإمكان الحصول على الحل المثالي للمسألة المعطاة بجمع الحلول المثالية للمسائل المتفرّعة عن المسألة الرئيسية. لحل المثال السابق دعنا نرمز للوزن بالرمز w وبما ان الحد المسموح به هو 10 كيلو جرام إذن w=10 .
أيضًا نرمز للعناصر بالرمز n. الخطوة الأولى للحل هو تكوين مصفوفة ثنائية الأبعاد أو بمعنى آخر جدول عدد صفوفه (n+1) وعدد أعمدته (w+1) يعني في مثالنا هذا سيكون عدد الصفوف (5+1=6) وذلك لأنه لدينا 5 عناصر بينما عدد الأعمدة (10+1=11) وذلك لأن أقصى وزن مسموح به 10.
يمثل رقم العمود j سعة وزن حقيبة الظهر الخاصة بنا. لذلك، القيم في العمود 5، على سبيل المثال، تفترض أن حقيبة الظهر الخاصة بنا يمكن أن تحتوي على 5 وحدات وزن. بعد ذلك نبدأ بملء الجدول بالقيم المحسوبة مع ملاحظة أن الصف رقم 0 يمثل الحالة التي لا يوجد لدينا عناصر للاختيار من بينها لذا يجب أن تكون القيمة القصوى التي يمكن تخزينها في أي حقيبة ظهر في هذه الحالة 0.
بالمثل، في العمود 0، بالنسبة للحقيبة التي يمكن أن تحتوي على 0 وحدة وزن، لذا فإن القيمة القصوى التي يمكن تخزينها فيه هي 0. أما بالنسبة لبقية الاعمدة والصفوف فنتبع التالي: لحساب الحد الأقصى للقيمة التي يمكننا الحصول عليها من العنصر i، نحتاج أولاً إلى مقارنة وزن العنصر i بسعة وزن الحقيبة.
من الواضح، إذا كان وزن العنصر أكبر مما يمكن أن تحمله الحقيبة، فلا يمكننا تضمينه، لذلك ليس من المنطقي إجراء الحساب. في هذه الحالة، يكون حل هذه المشكلة هو ببساطة القيمة القصوى التي يمكننا الحصول عليها بدون العنصر i (أي القيمة الموجودة في الصف أعلاه، في نفس العمود). ومع ذلك، لنفترض أن وزن هذا العنصر أقل من سعة حقيبة الظهر.
بالتالي لدينا خيار إدراجه، إذا كان من المحتمل أن يؤدي إلى زيادة الحد الأقصى للقيمة التي يمكن الحصول عليها. وبالتالي، فإن الحد الأقصى للقيمة التي يمكن الحصول عليها من خلال تضمين العنصر i هو = قيمة العنصر i نفسه + القيمة القصوى التي يمكن الحصول عليها مع السعة المتبقية من الحقيبة. بمعنى آخر، نريد الاستفادة الكاملة من سعة حقيبة الظهر الخاصة بنا وعدم ترك أي سعة متبقية تذهب سدى.
وبتطبيق ما سبق على المثال السابق نتحصل على الجدول الآتي:
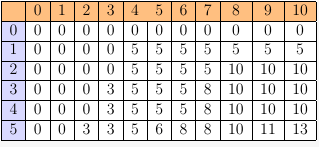
من الجدول نلاحظ أن أقصى قيمة تحصلنا عليها هي 13 والتي تنتج من جمع قيمة العنصر الثاني (10دولار) مع العنصر الخامس (3دولار) والذان في نفس الوقت لم يتجاوزا الوزن المسموح به 10 كيلو جرام.
ما أهمية خورزميات البرمجة الديناميكية؟
تكمن أهمية خوارزميات البرمجة الديناميكية في تقليل الوقت المستغرق لحساب المسائل الرياضية إذ تعمل على تخزين قيم هذه المسائل الفرعية وفي كل مرة تُصادف فيه المسألة الفرعية مرة أخرى، فإنها تبحث فقط عن القيمة بينما الخوارزميات العودية تعمل على تنفيذ ذلك بشكل متكرر، مع الاستمرار في استدعاء الوظيفة في كل مرة احتجنا إلى القيم السابقة. لمتابعة الأجزاء السابقة من سلسلة تعلم الخوارزميات اضغط هنا وهنا وهنا.
المصادر
brilliant.org
smithsonian magazine
geeksforgeeks 1
geeksforgeeks 2
plus.maths
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.



التعليقات :