محتويات المقال :
الرياضيات بين الماضي والحاضر
يُقال أن الرياضيات هي اللغة التي كتب بها الكون، بعض أفرع هذا العلم اكتشفت منذ الالاف السنين كالحساب والهندسة بينما البعض الآخر يُعد حديث الظهور نسبيًا كالتفاضل والتكامل وعلم الاحتمالات والهندسة التحليلية. إذا أتيح لك عزيزي القارئ السفر عبر الزمن إلى بدايات القرن السابع عشر ستلاحظ أن أعداد الكتب والمؤلفات المتعلقة بالرياضيات كانت شحيحة، ولكن هذا الوضع تغير تمامًا مع ظهور عالم الرياضيات الفرنسي دي فيرما الذي يُعد الأب الروحي لنظرية الاحتمالات والنظرية الحديثة للأعداد.
نشأته
ولد دي فيرما في السابع من أغسطس عام 1601 في مدينة بومنت دي لومان في فرنسا وتلقى تعليمه الابتدائي في مدرسة فرنسيسكيان المحلية وفيما بعد درس القانون في مدينة تولوز أو في مدينة بوردو حسب بعض الروايات. كان فيرما متبحرًا في شتى مجالات العلوم والأعمال الأدبية وأيضًا اللغات. ومن خلال دراسته لنظام الإحداثيات القديمة توصل إلى أن مجموعات النقاط ذات الخصائص المعينة، يمكن تسهيلها من خلال تطبيق الجبر على الهندسة من خلال نظام الإحداثيات الذي عرف فيما بعد بنظام الإحداثيات الكارتيزية التي يمكن التعبير بواسطتها عن الأشكال الهندسية باستعمال معادلات جبرية، وهي معادلات توافق إحداثيات النقاط الممثّلة للشكل الهندسي. وفي عام 1631 حصل فيرما على شهادة البكالوريا في القانون من جامعة أورليانز. وعمل في البرلمان المحلي في تولوز، وأصبح مستشارًا في عام 1634.
أهم أعمال دي فيرما
توصل العالم فيرما من خلال دراسته للمنحنيات إلى معادلة القطع المكافئ الشهيرة. ويعرف القطع المكافئ بأنه قطع مخروطي اختلافه المركزي يساوي الواحد الصحيح؛ نتيجة لذلك تكون كل القطوع المكافئة متشابهة بمعنى أن لها نفس الشكل مهما تغير حجمه. للقطع المكافئ العديد من التطبيقات في الحياة العملية فمثًلا أطباق أجهزة الإرسال والاستقبال الرادوية تُصمم على شكل قطع مكافئ بحيث تتركز الموجات الكهرومغناطيسية في نقطة محددة. وأيضًا توصل العالم فيرما إلى معادلة القطع الناقص وهو المنحنى الذي يكون اختلافه المركزي أكبر من الواحد الصحيح أو بعبارة أخرى هو المنحنى الذي يحقق الخاصية التالية: مجموعة النقاط التي تتميز بكون فرق مسافة هذه النقاط عن نقطتين ثابتتين ( تدعى البؤرتين ) هو عدد ثابت. يمكنك ملاحظة شكل القطع الناقص عندما تقذف حجرين في وقت واحد في بركة مياه راكدة ، ستلاحظ أن التموجات تتجه إلى الخارج في دوائر متحدة المركز. تتقاطع هذه الدوائر في نقاط لتشكل منحنى يعرف باسم القطع الناقص. و تظهر جليًا تطبيقات القطع الزئد في مجال الهندسة حيث تُصمم أبراج تبريد المفاعلات النووعية على شكل قطع ناقص وذلك لتعزيز مقاومتها للرياح ولتقليل تكلفة البناء.

تُصمم أبراج تبريد المفاعلات النووية على شكل قطع زائد
تطويره لنظرية الأعداد
سعى العالم فيرما لإقناع باسكال بالانضمام إليه في البحث في نظرية الأعداد. ومن خلال دراسته لكتاب «حساب ديوفانتوس-diophantus arithmetica»-عالم رياضيات يوناني عاش في القرن الثالث الميلادي- ،اكتشف فيرما نتائج جديدة في ما يعرف بالحساب المتقدم، العديد من النتائج التي توصل إليها كانت تتعلق بخصائص الأعداد الأولية وهي الأعداد الصحيحة الموجبة الأكبر من العدد واحد، والتي تقبل القسمة على عددين فقط هما العدد نفسه والواحد دون باقٍ؛ مثل الأعداد 5، 7، 11 ومن أجمل النتائج التي توصل إليها النظرية القائلة بأن أي عدد أولي ناتج من هذه العلاقة 4n + 1 يمكن التعبير عنه بشكل فريد كمجموع مربعين مثلا العدد 13 يمكن التعبير عنه بالعلاقة السابقة بالتعويض عن قيمة n بالعدد 3 (1+3×4) والذي يمكن التعبير عنه كمجموع مربعين كالتالي (2^2+2^3).

كتاب الحساب للعالم الاغريقي ديوفانتوس
مبرهنة فيرما الأخيرة
بالرغم من أن فيرما عالم رياضي إلا أنه كان يعمل في مجال القضاء في فرنسا وكانت الرياضيات هوايته المفضلة إذ كان يعكف على حل المسائل في كل مساء عند عودته من العمل. وفي ذات ليلة خطر على باله تساؤل حول معادلة شبيه بمعادلة فيثاغورس للمثلث القائم (X^2 +Y^2= Z^2) وكان يبحث عن الحلول الكلية للأعداد لتلك المعادلة وبالطبع هناك عدد لا نهائي من الأرقام الطبيعية التي يمكن التعويض بها في تلك المعادلة بصورة صحيحة (2^3+2^4= 2^5) و (2^6+2^8=2^10) ….إلخ. في تلك اللحظة سأل فيرما نفسه: ماذا لو قمت بتعديل هذه المعادلة فبدلًا عن استخدام الأس التربيعي، نستخدم الأس التكعيبي أو الأس الرابع أو الخامس وبشكل عام أس المعادلة أكبر من العدد 2 (n>2)، فهل توجد حلول لتلك المعادلات أو بمعنى آخر هل هذه المعادلة مثًلا صحيحة إذا كانت قيمة الأس أكبر من العدد 2 (X^n +Y^n= Z^n)؟ انهمك فيرما في التفكير لإجاد حلول لتلك المعادلات ولكنه لم يجد حلول لتلك المعادلات وعندئذ اعتقد بأنه توصل إلى إثبات أنه لا يوجد حلول لتلك المعادلات بلا أدنى شك. وفي ذلك شيء من الغرابة عزيزي القارئ: لماذا يوجد عدد لانهائي من الحلول للمعادلة ذات الأس التربيعي بينما لا يوجد أي حل لتلك المعادلات اللانهائية المرفوعة لأي أس أكبر من الرقم 2؟ الجدير بالذكر أن فيرما توصل لذلك الاثبات بنفسه وكتب تعليق موجز على هامش احدى صفحات نسخته من كتاب حساب ديوفانتوس حيث يقول: ” اكتشفت برهنًا رائعًا لهذه الفرضية ولكن الهامش لا يتسع لكتابته”. كلّف ذلك الهامش الضيق علماء الرياضيات من بعده حوالي 350 عامًا حتى يتوصلوا لذلك الإثبات من جديد. وأخيرًا تمكن عالم رياضيات البريطاني أندرو وايلز من إثبات فرضية فيرما بين عامي 1993 و 1995 والذي توج بجائزة الأكاديمية النرويجية للعلوم والآداب في عام 2016 تكريمًا لجهوده والتي يعتبرها البعض جائزة نوبل للرياضيات وحصل على مكافئة مالية تُقدر بسبعين ألف دولار.
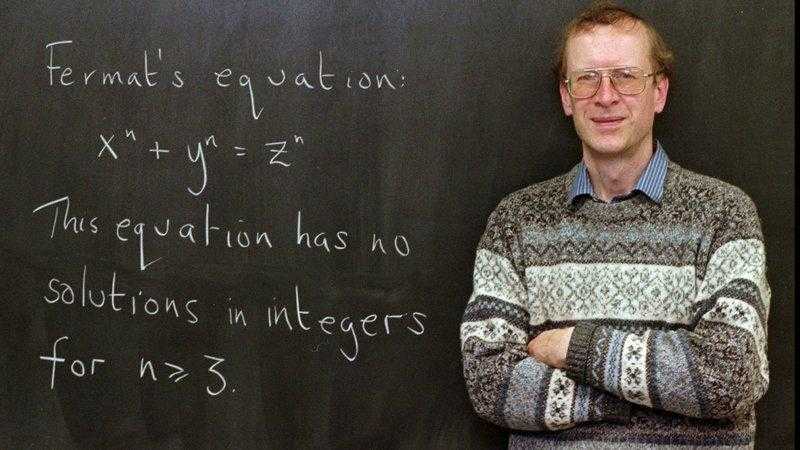
أندرو وايلز بجانب مبرهنة فيرما الأخيرة
المصادر
سعدنا بزيارتك، جميع مقالات الموقع هي ملك موقع الأكاديمية بوست ولا يحق لأي شخص أو جهة استخدامها دون الإشارة إليها كمصدر. تعمل إدارة الموقع على إدارة عملية كتابة المحتوى العلمي دون تدخل مباشر في أسلوب الكاتب، مما يحمل الكاتب المسؤولية عن مدى دقة وسلامة ما يكتب.



التعليقات :